题目内容
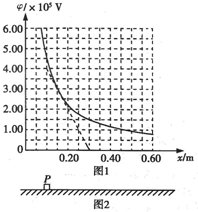 粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,且沿x轴方向的电势φ与坐标值x的关系如下表格所示.
粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,且沿x轴方向的电势φ与坐标值x的关系如下表格所示.| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| x/m | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 |
| φ/105v | 9.00 | 4.50 | 3.00 | 2.25 | 1.80 | 1.50 | 1.29 | 1.13 | 1.00 |
(1)由表格中的数据和图象给出的信息,写出沿x轴的电势φ与坐标值x的函数关系表达式.
(2)若将滑块无初速度地放在x=0.10m处,求滑块最终停止在何处?
(3)在上述第(2)问的整个运动过程中,它的加速度如何变化?当它位于x=0.15m时它的加速度多大?(电场中某点场强为φ-x图线上该点对应的斜率)
分析:(1)电势φ与坐标x图象是一条曲线,则φ与x关系可能是反比关系,即φ∝x-1;也可能φ与x2关系可能是反比关系,即φ∝x-2;…,依此类推,直到找到关系为止;
(2)滑块运动过程中,只有电场力和滑动摩擦力做功,根据动能定理列式求解即可;
(3)由于图象的切线的斜率表示电场强度,故场强逐渐变小,电场力逐渐变小;
电场力大于摩擦力时,物体加速,当电场力减小到等于摩擦力时,速度最大,此后电场力小于摩擦力,故物体开始减速,即滑块先由静到动,后由动到静,故先加速后减速;
(2)滑块运动过程中,只有电场力和滑动摩擦力做功,根据动能定理列式求解即可;
(3)由于图象的切线的斜率表示电场强度,故场强逐渐变小,电场力逐渐变小;
电场力大于摩擦力时,物体加速,当电场力减小到等于摩擦力时,速度最大,此后电场力小于摩擦力,故物体开始减速,即滑块先由静到动,后由动到静,故先加速后减速;
解答:解:(1)由数据表格和图象可得,电势?与x成反比关系,即φ=
;
当x=0.1m时,电势φ=4.5V,代入上述公式,得到k=4.5×104
故沿x轴的电势?与x的函数关系表达式?=
V.
(2)滑块运动的全部过程中,只有电场力和摩擦力做功,由动能定理得
WF+Wf=△EK=0
设滑块停止的位置为x2,有
q(?1-?2)-μmg(x2-x)=0
即q(
-
)-μmg(x2-x)=0
代入数据有
1.0×10-7(
-
)-0.20×0.10×10(x2-0.1)=0
可解得x2=0.225m(舍去x2=0.1m)
故滑块最终停止在坐标为0.225m的位置.
(3)先做加速度减小的加速运动,后做加速度增大的减速运动.
即加速度先减小后增大.
当它位于x=0.15m时,图象上该点的切线斜率表示场强大小
E=
=
N/C=2.0×106 N/C
滑块在该点的水平合力FX=Eq-μmg=2.0×106×1.0×10-7-0.20×0.10×10=0
故滑块的加速度a=
=0
故在上述第(2)问的整个运动过程中,它的加速度先变小后变大;当它位于x=0.15m时它的加速度为零.
答:(1)由表格中的数据和图象给出的信息,写出沿x轴的电势φ与坐标值x的函数关系表达式为?=
V.
(2)若将滑块无初速度地放在x=0.10m处,则滑块最终停止在最终停止在坐标为0.225m的位置;
(3)在上述第(2)问的整个运动过程中,它的加速度先变小后变大;当它位于x=0.15m时它的加速度为零.
| k |
| x |
当x=0.1m时,电势φ=4.5V,代入上述公式,得到k=4.5×104
故沿x轴的电势?与x的函数关系表达式?=
| 4.5×104 |
| x |
(2)滑块运动的全部过程中,只有电场力和摩擦力做功,由动能定理得
WF+Wf=△EK=0
设滑块停止的位置为x2,有
q(?1-?2)-μmg(x2-x)=0
即q(
| 4.5×104 |
| x |
| 4.5×104 |
| x2 |
代入数据有
1.0×10-7(
| 4.5×104 |
| 0.1 |
| 4.5×104 |
| x2 |
可解得x2=0.225m(舍去x2=0.1m)
故滑块最终停止在坐标为0.225m的位置.
(3)先做加速度减小的加速运动,后做加速度增大的减速运动.
即加速度先减小后增大.
当它位于x=0.15m时,图象上该点的切线斜率表示场强大小
E=
| ? |
| x |
| 3×105 |
| 0.15 |
滑块在该点的水平合力FX=Eq-μmg=2.0×106×1.0×10-7-0.20×0.10×10=0
故滑块的加速度a=
| Fx |
| m |
故在上述第(2)问的整个运动过程中,它的加速度先变小后变大;当它位于x=0.15m时它的加速度为零.
答:(1)由表格中的数据和图象给出的信息,写出沿x轴的电势φ与坐标值x的函数关系表达式为?=
| 4.5×104 |
| x |
(2)若将滑块无初速度地放在x=0.10m处,则滑块最终停止在最终停止在坐标为0.225m的位置;
(3)在上述第(2)问的整个运动过程中,它的加速度先变小后变大;当它位于x=0.15m时它的加速度为零.
点评:本题首先要明确φ-x图象中任意一点的切线的斜率表示电场强度的大小,由于是变加速运动,然后对各个过程分别运用动能定理列式求解.

练习册系列答案
相关题目
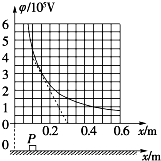 如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,在x轴上的电势φ与坐标x的关系用如图所示曲线表示,图中斜线为该曲线过点(0.15,3)的切线.现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视为质点),从x=0.10m处由静止释放,其与水平面的动摩擦因数为0.02.设最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2.则下列说法中正确的是( )
如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,在x轴上的电势φ与坐标x的关系用如图所示曲线表示,图中斜线为该曲线过点(0.15,3)的切线.现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视为质点),从x=0.10m处由静止释放,其与水平面的动摩擦因数为0.02.设最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2.则下列说法中正确的是( )| A、滑块运动的加速度逐渐减小 | B、滑块运动的加速度先减小后增大 | C、x=0.15m处的场强大小为2.0×106N/C | D、滑块运动的最大速度约为0.1m/s |

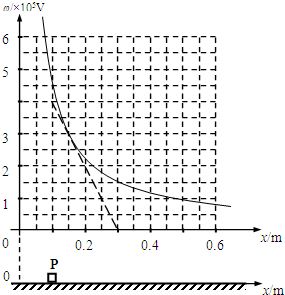 如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,且沿x轴方向的电势?与坐标值x的关系可用图中曲线表示,图中斜线为该曲线过点(0.15,3)的切线.现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视作质点),从x=0.10m处无初速释放,其与水平面的动摩擦因素为0.02.则下列说法正确的是( )
如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,且沿x轴方向的电势?与坐标值x的关系可用图中曲线表示,图中斜线为该曲线过点(0.15,3)的切线.现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视作质点),从x=0.10m处无初速释放,其与水平面的动摩擦因素为0.02.则下列说法正确的是( )