题目内容
粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,且沿x轴方向的电势?与坐标值x的关系如下表格所示:
根据上述表格中的数据可作出如右的?-x图象.现有一质量为0.10kg,电荷量为1.0×10-7C带正电荷的滑块(可视作质点),其与水平面的动摩擦因素为0.20.问:
(1)由数据表格和图象给出的信息,写出沿x轴的电势?与x的函数关系表达式.
(2)若将滑块无初速地放在x=0.10m处,则滑块最终停止在何处?
(3)在上述第(2)问的整个运动过程中,它的加速度如何变化?当它位于x=0.15m时它的加速度多大?
(4)若滑块从x=0.60m处以初速度v0沿-x方向运动,要使滑块恰能回到出发点,其初速度v0应为多大?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| x/m | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 |
| φ/105v | 9.00 | 4.50 | 3.00 | 2.25 | 1.80 | 1.50 | 1.29 | 1.13 | 1.00 |
(1)由数据表格和图象给出的信息,写出沿x轴的电势?与x的函数关系表达式.
(2)若将滑块无初速地放在x=0.10m处,则滑块最终停止在何处?
(3)在上述第(2)问的整个运动过程中,它的加速度如何变化?当它位于x=0.15m时它的加速度多大?
(4)若滑块从x=0.60m处以初速度v0沿-x方向运动,要使滑块恰能回到出发点,其初速度v0应为多大?

分析:(1)电势φ与坐标x图象是一条曲线,则φ与x关系可能是反比关系,即φ∝x-1;也可能φ与x2关系可能是反比关系,即φ∝x-2;…,依此类推,直到找到关系为止;
(2)滑块运动过程中,只有电场力和滑动摩擦力做功,根据动能定理列式求解即可;
(3)由于图象的切线的斜率表示电场强度,故场强逐渐变小,电场力逐渐变小;
电场力大于摩擦力时,物体加速,当电场力减小到等于摩擦力时,速度最大,此后电场力小于摩擦力,故物体开始减速,即滑块先由静到动,后由动到静,故先加速后减速;
(4)滑块运动到最左端位置时速度为零;滑块向左运动过程中,电场力做负功,摩擦力做负功;滑块向右运动过程中,电场力做正功,摩擦力做负功;对滑块运动的全部过程和向右运动的过程分别运用动能定理列式求解即可.
(2)滑块运动过程中,只有电场力和滑动摩擦力做功,根据动能定理列式求解即可;
(3)由于图象的切线的斜率表示电场强度,故场强逐渐变小,电场力逐渐变小;
电场力大于摩擦力时,物体加速,当电场力减小到等于摩擦力时,速度最大,此后电场力小于摩擦力,故物体开始减速,即滑块先由静到动,后由动到静,故先加速后减速;
(4)滑块运动到最左端位置时速度为零;滑块向左运动过程中,电场力做负功,摩擦力做负功;滑块向右运动过程中,电场力做正功,摩擦力做负功;对滑块运动的全部过程和向右运动的过程分别运用动能定理列式求解即可.
解答:解:(1)由数据表格和图象可得,电势?与x成反比关系,即φ=
;
当x=0.1m时,电势φ=4.5V,代入上述公式,得到k=4.5×104
故沿x轴的电势?与x的函数关系表达式?=
V.
(2)滑块运动的全部过程中,只有电场力和摩擦力做功,由动能定理得
WF+Wf=△EK=0
设滑块停止的位置为x2,有
q(?1-?2)-μmg(x2-x)=0
即q(
-
)-μmg(x2-x)=0
代入数据有
1.0×10-7(
-
)-0.20×0.10×10(x2-0.1)=0
可解得x2=0.225m(舍去x2=0.1m)
故滑块最终停止在坐标为0.225m的位置.
(3)先做加速度减小的加速运动,后做加速度增大的减速运动.
即加速度先减小后增大.
当它位于x=0.15m时,图象上该点的切线斜率表示场强大小
E=
=
=2.0×106N/C
滑块在该点的水平合力FX=Eq-μmg=2.0×106×1.0×10-7-0.20×0.10×10=0
故滑块的加速度a=
=0
故在上述第(2)问的整个运动过程中,它的加速度先变小后变大;当它位于x=0.15m时它的加速度为零.
(4)设滑块到达的最左侧位置为x1,则滑块由该位置返回到出发点的过程中
由动能定理 WF+Wf=△EK=0
有 q(?1-?2)-μmg(x-x1)=0
代入数据有 1.0×10-7(
-
)-0.20×0.10×10(0.6-x1)=0
可解得x1=0.0375m(舍去x1=0.6m).
再对滑块从开始运动到返回出发点的整个过程,由动能定理
-2μmg(x-x1)=0-
mv02
代入数据有2×0.20×0.10×10(0.60-0.0375)=0.5×0.10v02
可解得v0=
≈2.12m/s
即滑块从x=0.60m处以初速度v0沿-x方向运动,要使滑块恰能回到出发点,其初速度v0应为2.12m/s.
| k |
| x |
当x=0.1m时,电势φ=4.5V,代入上述公式,得到k=4.5×104
故沿x轴的电势?与x的函数关系表达式?=
| 4.5×104 |
| x |
(2)滑块运动的全部过程中,只有电场力和摩擦力做功,由动能定理得
WF+Wf=△EK=0
设滑块停止的位置为x2,有
q(?1-?2)-μmg(x2-x)=0
即q(
| 4.5×104 |
| x |
| 4.5×104 |
| x2 |
代入数据有
1.0×10-7(
| 4.5×104 |
| 0.1 |
| 4.5×104 |
| x2 |
可解得x2=0.225m(舍去x2=0.1m)
故滑块最终停止在坐标为0.225m的位置.
(3)先做加速度减小的加速运动,后做加速度增大的减速运动.
即加速度先减小后增大.
当它位于x=0.15m时,图象上该点的切线斜率表示场强大小
E=
| ? |
| x |
| 3.00×105 |
| 0.15 |
滑块在该点的水平合力FX=Eq-μmg=2.0×106×1.0×10-7-0.20×0.10×10=0
故滑块的加速度a=
| Fx |
| m |
故在上述第(2)问的整个运动过程中,它的加速度先变小后变大;当它位于x=0.15m时它的加速度为零.
(4)设滑块到达的最左侧位置为x1,则滑块由该位置返回到出发点的过程中
由动能定理 WF+Wf=△EK=0
有 q(?1-?2)-μmg(x-x1)=0
代入数据有 1.0×10-7(
| 4.5×104 |
| x1 |
| 4.5×104 |
| 0.6 |
可解得x1=0.0375m(舍去x1=0.6m).
再对滑块从开始运动到返回出发点的整个过程,由动能定理
-2μmg(x-x1)=0-
| 1 |
| 2 |
代入数据有2×0.20×0.10×10(0.60-0.0375)=0.5×0.10v02
可解得v0=
| 3 |
| 2 |
| 2 |
即滑块从x=0.60m处以初速度v0沿-x方向运动,要使滑块恰能回到出发点,其初速度v0应为2.12m/s.
点评:本题首先要明确φ-x图象中任意一点的切线的斜率表示电场强度的大小,由于是变加速运动,然后对各个过程分别运用动能定理列式求解.

练习册系列答案
相关题目
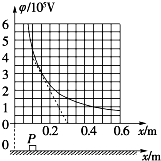 如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,在x轴上的电势φ与坐标x的关系用如图所示曲线表示,图中斜线为该曲线过点(0.15,3)的切线.现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视为质点),从x=0.10m处由静止释放,其与水平面的动摩擦因数为0.02.设最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2.则下列说法中正确的是( )
如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,在x轴上的电势φ与坐标x的关系用如图所示曲线表示,图中斜线为该曲线过点(0.15,3)的切线.现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视为质点),从x=0.10m处由静止释放,其与水平面的动摩擦因数为0.02.设最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2.则下列说法中正确的是( )| A、滑块运动的加速度逐渐减小 | B、滑块运动的加速度先减小后增大 | C、x=0.15m处的场强大小为2.0×106N/C | D、滑块运动的最大速度约为0.1m/s |
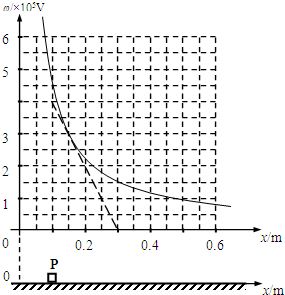 如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,且沿x轴方向的电势?与坐标值x的关系可用图中曲线表示,图中斜线为该曲线过点(0.15,3)的切线.现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视作质点),从x=0.10m处无初速释放,其与水平面的动摩擦因素为0.02.则下列说法正确的是( )
如图所示,粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,且沿x轴方向的电势?与坐标值x的关系可用图中曲线表示,图中斜线为该曲线过点(0.15,3)的切线.现有一质量为0.20kg,电荷量为+2.0×10-8C的滑块P(可视作质点),从x=0.10m处无初速释放,其与水平面的动摩擦因素为0.02.则下列说法正确的是( )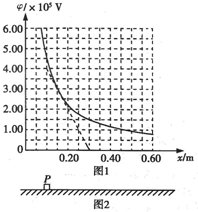 粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,且沿x轴方向的电势φ与坐标值x的关系如下表格所示.
粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x轴平行,且沿x轴方向的电势φ与坐标值x的关系如下表格所示.