题目内容
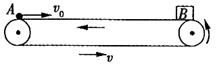
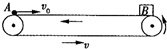
如图所示,长L=34.5m的水平传送带以大小为υ=3m/s的速度沿逆时针方向运动,将一质量为M=2kg的小木盒B轻轻放在传送带右端,B与传送带之间的动摩擦因数μ=0.3,在木盒放上传送带的同时,有一个光滑的质量为m=1kg的小球A自传送带的左端以υ=15m/s的速度在传送带上向右运动.球与木盒相遇时,木盒与传送带已相对静止,相遇后球立即进入盒中与盒保持相对静止.(取g=10m/s2)求:(1)球与木盒相遇后瞬间,两者共同运动的速度;
(2)小木盒从传送带右端到左端的时间;
(3)小木盒从传送带右端到左端的过程中因木盒与传送带间的摩擦而产生的热量.
【答案】分析:(1)小球是光滑的,在传送带不受摩擦力,做匀速运动.球与木盒相遇时,木盒与传送带已相对静止,木盒的速度等于传送带的速度,根据碰撞过程动量守恒,求出相遇后瞬间两者共同运动的速度;
(2)分析小木盒的运动过程,分段求时间.小木盒B放在传送带右端后在滑动摩擦力作用下先向左加速运动,后做匀速运动.根据牛顿定律和位移关系求出小木盒加速运动和匀速运动到两物相遇的时间.相遇后先向右做匀减速运动,再向左做匀加速运动,最后与传送带一起做匀速运动,由牛顿定律和运动学结合求解时间.再求出总时间.
(3)木盒与传送带间的摩擦产生的热量等于滑动摩擦力大小与两者相对滑动距离的乘积,分别求出各个过程中两者相对滑动的距离,求出因摩擦而产生的热量,再求解总热量.
解答:解:(1)选向右的方向为正方向,则在相遇前瞬间,小木盒B的速度为vB=v=3m/s.设相遇后两者共同的速度为v′,由动量守恒得到:
mv-MvB=(m+M)v′
解得:v′=3m/s,方向向右.
(2)小木盒B放在传送带右端后在滑动摩擦力作用下先向左加速运动,滑动摩擦力f1=μMg=6N,加速度a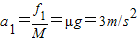 ,经过
,经过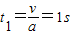 ,小木盒在传送带上做匀速运动.
,小木盒在传送带上做匀速运动.
小球向右匀速运动,设经过时间t二者相遇,则有
vt+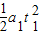 +v(t-t1)=L
+v(t-t1)=L
解得:t=2s
小木盒在传送带加速运动的位移s1=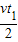 =1.5m
=1.5m
匀速运动的时间t2=t-t1=1s,位移s2=vt2=3m
相遇后先向右做匀减速运动,所受滑动摩擦力:f2=μ(m+M)g=9N,加速度为:a2=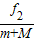 =μg=3m/s2,向右减速运动的时间:
=μg=3m/s2,向右减速运动的时间:
t3=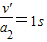
再向左做加速运动,加速运动的时间:
t4=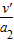 =
=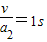
最后与传送带一起匀速运动,匀速运动时间为:
t5=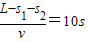
所以小木盒从传送带右端到左端的时间为t=t1+t2+t3+t4+t5=14s
(3)①小木盒在t1时间内相对传送带滑动距离为:x1=vt1-s1=1.5m
产生热量:Q1=f1x1=μMgx1=9J
②向右减速运动相对地向右位移x=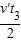 =1.5m
=1.5m
相对传动带滑动距离为:x2=vt3+x=4.5m
产生热量:Q2=f2x2=μ(m+M)gx2=40.5J
③向左加速运动的位移: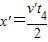 =1.5m
=1.5m
相对传送带滑动距离为: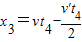 =1.5m
=1.5m
产生热量:Q3=f2x3=μ(m+M)gx3=13.5J
所以因木盒与传送带间的摩擦而产生的热量:Q=Q1+Q2+Q3=63J
答:(1)球与木盒相遇后瞬间,两者共同运动的速度为3m/s,方向向右.
(2)小木盒从传送带右端到左端的时间为14s;
(3)小木盒从传送带右端到左端的过程中因木盒与传送带间的摩擦而产生的热量为63J.
点评:本题中物理过程比较复杂,基本方法不变,还是分析物体的受力情况和运动情况.摩擦生热等于滑动摩擦力大小与物体间相对滑动距离的乘积.考验考生的细心和耐心.
(2)分析小木盒的运动过程,分段求时间.小木盒B放在传送带右端后在滑动摩擦力作用下先向左加速运动,后做匀速运动.根据牛顿定律和位移关系求出小木盒加速运动和匀速运动到两物相遇的时间.相遇后先向右做匀减速运动,再向左做匀加速运动,最后与传送带一起做匀速运动,由牛顿定律和运动学结合求解时间.再求出总时间.
(3)木盒与传送带间的摩擦产生的热量等于滑动摩擦力大小与两者相对滑动距离的乘积,分别求出各个过程中两者相对滑动的距离,求出因摩擦而产生的热量,再求解总热量.
解答:解:(1)选向右的方向为正方向,则在相遇前瞬间,小木盒B的速度为vB=v=3m/s.设相遇后两者共同的速度为v′,由动量守恒得到:
mv-MvB=(m+M)v′
解得:v′=3m/s,方向向右.
(2)小木盒B放在传送带右端后在滑动摩擦力作用下先向左加速运动,滑动摩擦力f1=μMg=6N,加速度a
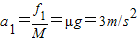 ,经过
,经过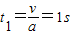 ,小木盒在传送带上做匀速运动.
,小木盒在传送带上做匀速运动.小球向右匀速运动,设经过时间t二者相遇,则有
vt+
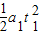 +v(t-t1)=L
+v(t-t1)=L 解得:t=2s
小木盒在传送带加速运动的位移s1=
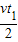 =1.5m
=1.5m匀速运动的时间t2=t-t1=1s,位移s2=vt2=3m
相遇后先向右做匀减速运动,所受滑动摩擦力:f2=μ(m+M)g=9N,加速度为:a2=
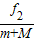 =μg=3m/s2,向右减速运动的时间:
=μg=3m/s2,向右减速运动的时间:t3=
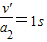
再向左做加速运动,加速运动的时间:
t4=
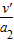 =
=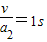
最后与传送带一起匀速运动,匀速运动时间为:
t5=
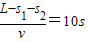
所以小木盒从传送带右端到左端的时间为t=t1+t2+t3+t4+t5=14s
(3)①小木盒在t1时间内相对传送带滑动距离为:x1=vt1-s1=1.5m
产生热量:Q1=f1x1=μMgx1=9J
②向右减速运动相对地向右位移x=
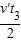 =1.5m
=1.5m相对传动带滑动距离为:x2=vt3+x=4.5m
产生热量:Q2=f2x2=μ(m+M)gx2=40.5J
③向左加速运动的位移:
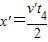 =1.5m
=1.5m相对传送带滑动距离为:
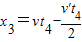 =1.5m
=1.5m产生热量:Q3=f2x3=μ(m+M)gx3=13.5J
所以因木盒与传送带间的摩擦而产生的热量:Q=Q1+Q2+Q3=63J
答:(1)球与木盒相遇后瞬间,两者共同运动的速度为3m/s,方向向右.
(2)小木盒从传送带右端到左端的时间为14s;
(3)小木盒从传送带右端到左端的过程中因木盒与传送带间的摩擦而产生的热量为63J.
点评:本题中物理过程比较复杂,基本方法不变,还是分析物体的受力情况和运动情况.摩擦生热等于滑动摩擦力大小与物体间相对滑动距离的乘积.考验考生的细心和耐心.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,长L=34.5m的水平传送带以大小为υ=3m/s的速度沿逆时针方向运动,将一质量为M=2kg的小木盒B轻轻放在传送带右端,B与传送带之间的动摩擦因数μ=0.3,在木盒放上传送带的同时,有一个光滑的质量为m=1kg的小球A自传送带的左端以υ0=15m/s的速度在传送带上向右运动.球与木盒相遇时,木盒与传送带已相对静止,相遇后球立即进入盒中与盒保持相对静止.(取g=10m/s2)求:
如图所示,长L=34.5m的水平传送带以大小为υ=3m/s的速度沿逆时针方向运动,将一质量为M=2kg的小木盒B轻轻放在传送带右端,B与传送带之间的动摩擦因数μ=0.3,在木盒放上传送带的同时,有一个光滑的质量为m=1kg的小球A自传送带的左端以υ0=15m/s的速度在传送带上向右运动.球与木盒相遇时,木盒与传送带已相对静止,相遇后球立即进入盒中与盒保持相对静止.(取g=10m/s2)求: