题目内容
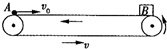
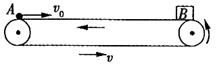
如图所示,长L=
(1)球与木盒相遇后瞬间,两者共同运动的速度;
(2)小木盒从传送带右端到左端的时间;
(3)小木盒从传送带右端到左端的过程中因木盒与传送带间的摩擦而产生的热量。
解:(1)设球与木盒相遇后瞬间,两者共同运动的速度为v1,由动量守恒定律
mv0-Mv=(m+M)v1①
代入数据,解得v1=
向右。③
(2)木盒运动加速度为a=μg=
设木盒从静止开始加速运动到与木盒相对静止时间为t1,位移为s1
t1=![]() =1 s④
=1 s④
s1=![]() at12=
at12=
设木盒从与木盒相对静止到与小球碰撞时间为t2,位移为s2
t2=![]() =1 s⑤
=1 s⑤
s2=vt2=
设木盒与小球碰后一起向右减速到静止的时间为t3,一起向左加速到与木盒相对静止的时间为t4
t3=![]() =1 s⑥
=1 s⑥
t4=![]() =1 s⑦
=1 s⑦
t3到t4时间内木盒的位移为0
木盒与小球一起匀速运动到传送带左端的时间为t5
t5=![]() =10 s⑧
=10 s⑧
总时间T=t1+t2+t3+t4+t5=14 s。⑨
(3)设木盒从静止开始加速运动到与木盒相对静止过程中相对位移为Δs1,产生的热为Q1,木盒与小球碰后一起向右减速到静止过程中相对位移为Δs2,产生的热为Q2,一起向左加速到与木盒相对静止过程相对位移为Δs3,产生的热为Q3
Δs1=vt1-s1=
Q1=μMgΔs1=9 J⑩
Δs2=vt3+![]() =
=
Q2=μ(M+m)gΔs2=40.5 J![]()
Δs3=vt4-![]() =
=
Q3=μ(M+m)gΔs3=13.5 J![]()
总热量Q=Q1+Q2+Q3=63 J。![]()

练习册系列答案
相关题目
 如图所示,长L=34.5m的水平传送带以大小为υ=3m/s的速度沿逆时针方向运动,将一质量为M=2kg的小木盒B轻轻放在传送带右端,B与传送带之间的动摩擦因数μ=0.3,在木盒放上传送带的同时,有一个光滑的质量为m=1kg的小球A自传送带的左端以υ0=15m/s的速度在传送带上向右运动.球与木盒相遇时,木盒与传送带已相对静止,相遇后球立即进入盒中与盒保持相对静止.(取g=10m/s2)求:
如图所示,长L=34.5m的水平传送带以大小为υ=3m/s的速度沿逆时针方向运动,将一质量为M=2kg的小木盒B轻轻放在传送带右端,B与传送带之间的动摩擦因数μ=0.3,在木盒放上传送带的同时,有一个光滑的质量为m=1kg的小球A自传送带的左端以υ0=15m/s的速度在传送带上向右运动.球与木盒相遇时,木盒与传送带已相对静止,相遇后球立即进入盒中与盒保持相对静止.(取g=10m/s2)求: