题目内容
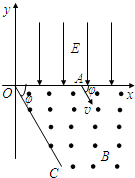 (2008?宁夏)如图所示,在xOy平面的第一象限有一匀强电场,电场的方向平行于y轴向下;在x轴和第四象限的射线OC之间有一匀强磁场,磁感应强度的大小为B,方向垂直于纸面向外.有一质量为m,带有电荷量+q的质点由电场左侧平行于x轴射入电场.质点到达x轴上A点时,速度方向与x轴的夹角为φ,A点与原点O的距离为d.接着,质点进入磁场,并垂直于OC飞离磁场.不计重力影响.若OC与x轴的夹角φ,求:
(2008?宁夏)如图所示,在xOy平面的第一象限有一匀强电场,电场的方向平行于y轴向下;在x轴和第四象限的射线OC之间有一匀强磁场,磁感应强度的大小为B,方向垂直于纸面向外.有一质量为m,带有电荷量+q的质点由电场左侧平行于x轴射入电场.质点到达x轴上A点时,速度方向与x轴的夹角为φ,A点与原点O的距离为d.接着,质点进入磁场,并垂直于OC飞离磁场.不计重力影响.若OC与x轴的夹角φ,求:(1)粒子在磁场中运动速度的大小;
(2)匀强电场的场强大小.
分析:(1)粒子在磁场中做匀速圆周运动,结合几何关系由洛仑兹力充当向心力可求得粒子在磁场中的速度;
(2)粒子在电场中做的是类平抛运动,对水平方向的匀速和竖直方向的匀加速分中别进行分析,根据牛顿第二定律及运动学公式可求得电场强度.
(2)粒子在电场中做的是类平抛运动,对水平方向的匀速和竖直方向的匀加速分中别进行分析,根据牛顿第二定律及运动学公式可求得电场强度.
解答: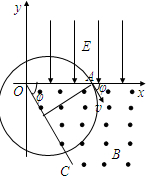 解:(1)由几何关系得:R=dsinφ
解:(1)由几何关系得:R=dsinφ
由洛仑兹力公式和牛顿第二定律得qvB=m
解得:v=
sinφ
(2)质点在电场中的运动为类平抛运动.设质点射入电场的速度为v0,在电场中的加速度为a,运动时间为t,则有:
v0=vcosφ
vsinφ=at
d=v0t
解得:a=
设电场强度的大小为E,由牛顿第二定律得
qE=ma
解得:E=
sin3φcosφ
答;(1)粒子在磁场中的速度为
sinφ;
(2)匀强电场的大小为E=
sin3φcosφ
 解:(1)由几何关系得:R=dsinφ
解:(1)由几何关系得:R=dsinφ由洛仑兹力公式和牛顿第二定律得qvB=m
| v2 |
| R |
解得:v=
| qBd |
| m |
(2)质点在电场中的运动为类平抛运动.设质点射入电场的速度为v0,在电场中的加速度为a,运动时间为t,则有:
v0=vcosφ
vsinφ=at
d=v0t
解得:a=
| v2sinφcosφ |
| d |
设电场强度的大小为E,由牛顿第二定律得
qE=ma
解得:E=
| qB2d |
| m |
答;(1)粒子在磁场中的速度为
| qBd |
| m |
(2)匀强电场的大小为E=
| qB2d |
| m |
点评:本题为电荷在电场和磁场中运动的题目,在电场中的运动一般以平抛为主,而在圆周运动中主要考查匀速圆周运动,应注意找出圆心和半径;同时要注意题目中哪些为已知量哪些为未知量.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

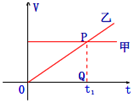 (2008?宁夏)甲乙两车在公路上沿同一方向做直线运动,它们的v-t图象如图所示.两图象在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t′,则下面四组t′和d的组合可能是( )
(2008?宁夏)甲乙两车在公路上沿同一方向做直线运动,它们的v-t图象如图所示.两图象在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t′,则下面四组t′和d的组合可能是( ) (2008?宁夏)一滑块在水平地面上沿直线滑行,t=0时其速度为1m/s.从此刻开始滑块运动方向上再施加一水平面作用F,力F和滑块的速度v随时间的变化规律分别如图a和图b所示.设在第1秒内、第2秒内、第3秒内力F对滑块做的功分别为W1、W2、W3,则以下关系正确的是( )
(2008?宁夏)一滑块在水平地面上沿直线滑行,t=0时其速度为1m/s.从此刻开始滑块运动方向上再施加一水平面作用F,力F和滑块的速度v随时间的变化规律分别如图a和图b所示.设在第1秒内、第2秒内、第3秒内力F对滑块做的功分别为W1、W2、W3,则以下关系正确的是( ) (2008?宁夏)如图所示,C为中间插有电介质的电容器,a和b为其两极板;a板接地;P和Q为两竖直放置的平行金属板,在两板间用绝缘线悬挂一带电小球;P板与b板用导线相连,Q板接地.开始时悬线静止在竖直方向,在b板带电后,悬线偏转了角度a.在以下方法中,能使悬线的偏角a变大的是( )
(2008?宁夏)如图所示,C为中间插有电介质的电容器,a和b为其两极板;a板接地;P和Q为两竖直放置的平行金属板,在两板间用绝缘线悬挂一带电小球;P板与b板用导线相连,Q板接地.开始时悬线静止在竖直方向,在b板带电后,悬线偏转了角度a.在以下方法中,能使悬线的偏角a变大的是( )