题目内容
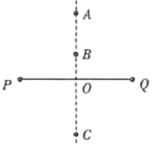
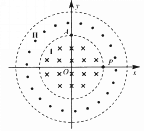
【题目】如图所示,为一磁约束装置的原理图,同心圆圆心O与xOy平面坐标系原点重合。半径为![]() 的圆形区域I内有方向垂直于xOy平面向里的匀强磁场。一束质量为m、电荷量为q、动能为
的圆形区域I内有方向垂直于xOy平面向里的匀强磁场。一束质量为m、电荷量为q、动能为![]() 的带正电粒子从坐标为(0,
的带正电粒子从坐标为(0, ![]() )的A点沿y轴负方向射入磁场区域I,粒子全部经过坐标为(
)的A点沿y轴负方向射入磁场区域I,粒子全部经过坐标为(![]() ,0)的P点,方向沿x轴正方向。当在环形区域II加上方向垂直于xOy平面向外的另一匀强磁场时,上述粒子仍从A点沿y轴负方向射入区域I,所有粒子恰好能够约束在环形区域内,且经过环形区域II的磁场偏转后第一次沿半径方向从区域II射入区域I时经过内圆周
,0)的P点,方向沿x轴正方向。当在环形区域II加上方向垂直于xOy平面向外的另一匀强磁场时,上述粒子仍从A点沿y轴负方向射入区域I,所有粒子恰好能够约束在环形区域内,且经过环形区域II的磁场偏转后第一次沿半径方向从区域II射入区域I时经过内圆周
上的M点(M点未画出)。不计重力和粒子间的相互作用。
(1)求区域I中磁感应强度![]() 的大小。
的大小。
(2)若环形区域II中磁感应强度![]() ,求M点坐标及环形外圆半径R。
,求M点坐标及环形外圆半径R。
(3)求粒子从A点沿y轴负方向射入圆形区域I至再次以相同速度经过A点的过程所通过的总路程。
【答案】(1)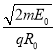 (2)
(2)![]() (3)
(3)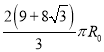
【解析】试题分析:(1)由题设条件就能求出粒子在Ⅰ区内做匀速圆周运动的半径,由洛仑兹力提供向心力就能求出Ⅰ区磁场的磁感应强度大小.(2)进入Ⅱ后,粒子恰好约束在该区,画出粒子运动轨迹,由两区域内磁场的关系,找到在Ⅱ区内做匀速圆周运动的半径,再由几何关系求得粒子在Ⅱ区内转过的圆心角,从而再由几何关系就能求出M点的坐标和环形的外圆半径.(3)先找出从A点出发,经过Ⅰ、Ⅱ区的正反两次偏转再次进入Ⅰ区时,相对OA方向偏转的角度,若经过m次偏转时,粒子第一次经过A点,此时转过m周,列出方程,解出整数解,那么总路程就是m倍的一次偏转的路程.
(1)由题意,粒子在区域Ⅰ内从A点做匀速圆周运动到P点,显然![]()
在磁场中,由洛伦兹力提供向心力,则有: ![]() ,且
,且![]()
联立解得: 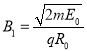
(2)粒子进入环形区域Ⅱ后做顺时针方向匀速圆周运动,则有: ![]()
由题设条件: ![]()
联立解得: ![]()
画出粒子在Ⅱ区内做匀速圆周运动的轨迹如图所示
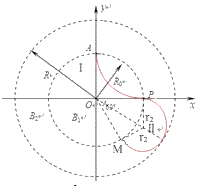
由几何关系得: ![]() ,则M点的坐标为
,则M点的坐标为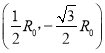
由几何关系外环的半径![]()
(3)粒子在Ⅰ区域和Ⅱ区域两次偏转后,从M点再次进入Ⅰ区域时,圆心角转过![]() ,设经过m次这样的偏转后第一次从A点再交入射,此时圆心角转过n个
,设经过m次这样的偏转后第一次从A点再交入射,此时圆心角转过n个![]()
则有:150m=360n(m、n取正整数)
解得:m=12,n=5.
而粒子在Ⅰ、Ⅱ区偏转一次通过的路程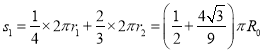
所以经过12次如此偏转后第一次通过A点,则总路程为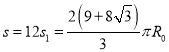

 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案