题目内容
 如图所示,相距为d、板间电压为U的平行金属板M、N间有垂直纸面向里、磁感应强度为B0的匀强磁场;在pOy区域内有垂直纸面向外、磁感应强度为B的匀强磁场;pOx区域为无场区.
如图所示,相距为d、板间电压为U的平行金属板M、N间有垂直纸面向里、磁感应强度为B0的匀强磁场;在pOy区域内有垂直纸面向外、磁感应强度为B的匀强磁场;pOx区域为无场区.一正离子沿平行于金属板、垂直磁场射入两板间并做匀速直线运动,从H(0,a)点垂直y轴进入第Ⅰ象限.
(1)求离子在平行金属板间的运动速度;
(2)若离子经Op上某点离开磁场,最后垂直x轴离开第Ⅰ象限,求离子在第Ⅰ象限磁场区域的运动时间;
(3)要使离子一定能打在x轴上,则离子的荷质比
| q | m |
分析:(1)正离子沿平行于金属板垂直磁场射入两板间做匀速直线运动时,洛伦兹力与电场力平衡,由平衡条件和E0=
结合可求出离子在平行金属板间的运动速度.
(2)离子在磁场中运动
圈后从Op上离开磁场,可求出离子在磁场中运动时间
,离开磁场后离子做匀速直线运动,由几何知识求出位移,即可求出时间.
(3)带电粒子进入pOy区域做匀速圆周运动,据题由几何关系可求出圆周运动的半径.在磁场中由洛伦兹力提供向心力,可求出比荷.
| U |
| d |
(2)离子在磁场中运动
| 1 |
| 4 |
| T |
| 4 |
(3)带电粒子进入pOy区域做匀速圆周运动,据题由几何关系可求出圆周运动的半径.在磁场中由洛伦兹力提供向心力,可求出比荷.
解答: 解:(1)离子在平行板内匀速直线运动,因此有 qvB0=qE
解:(1)离子在平行板内匀速直线运动,因此有 qvB0=qE
又E=
解得离子在平行板内的速度为v=
(2)如图为离子在第I象限磁场区域内运动的轨迹图,
由几何关系得,轨迹半径为r=
,
轨迹对应的圆心角为θ=
运动周期为T=
=
运动时间为t=
?T=
?T=
(3)要使离子一定能打在x轴上,离子在磁场B中运动的最小半径如图所示

由几何关系r2+
r2=a 得r2=
由qvB=
得
=
=(1+
)
即
必须小于(1+
)
.
答:(1)离子在平行金属板间的运动速度v=
;
(2)离子在第Ⅰ象限磁场区域的运动时间t=
;
(3)要使离子一定能打在x轴上,则离子的荷质比
应小于(1+
)
.
 解:(1)离子在平行板内匀速直线运动,因此有 qvB0=qE
解:(1)离子在平行板内匀速直线运动,因此有 qvB0=qE 又E=
| U |
| d |
解得离子在平行板内的速度为v=
| U |
| dB0 |
(2)如图为离子在第I象限磁场区域内运动的轨迹图,
由几何关系得,轨迹半径为r=
| a |
| 2 |
轨迹对应的圆心角为θ=
| π |
| 2 |
运动周期为T=
| 2πr |
| v |
| πadB0 |
| U |
运动时间为t=
| θ |
| 2π |
| 1 |
| 4 |
| πadB0 |
| 4U |
(3)要使离子一定能打在x轴上,离子在磁场B中运动的最小半径如图所示

由几何关系r2+
| 2 |
| a | ||
1+
|
由qvB=
| mv2 |
| r2 |
| q |
| m |
| v |
| Br2 |
| 2 |
| U |
| dB0Ba |
即
| q |
| m |
| 2 |
| U |
| dB0Ba |
答:(1)离子在平行金属板间的运动速度v=
| U |
| dB0 |
(2)离子在第Ⅰ象限磁场区域的运动时间t=
| πadB0 |
| 4U |
(3)要使离子一定能打在x轴上,则离子的荷质比
| q |
| m |
| 2 |
| U |
| dB0Ba |
点评:本题中离子在复合场中运动的问题是速度选择器的模型,要比较熟悉.在磁场中画轨迹,由几何知识求解半径、由圆心角确定时间都是常规思路.

练习册系列答案
相关题目
 (2011?广州一模)如图所示,相距为d、板间电压为U的平行金属板M、N间有垂直纸面向里、磁感应强度为B0的匀强磁场;在pOy区域内有垂直纸面向外、磁感应强度为B的匀强磁场;pOx区域为无场区.一正离子(不计重力)沿平行于金属板、垂直磁场射入两板间并做匀速直线运动,从H(0,a)点垂直y轴进入第Ⅰ象限,经Op上某点离开磁场,最后垂直x轴离开第Ⅰ象限.求:
(2011?广州一模)如图所示,相距为d、板间电压为U的平行金属板M、N间有垂直纸面向里、磁感应强度为B0的匀强磁场;在pOy区域内有垂直纸面向外、磁感应强度为B的匀强磁场;pOx区域为无场区.一正离子(不计重力)沿平行于金属板、垂直磁场射入两板间并做匀速直线运动,从H(0,a)点垂直y轴进入第Ⅰ象限,经Op上某点离开磁场,最后垂直x轴离开第Ⅰ象限.求: 如图所示,相距为d的两根直木棍AB和CD相互平行,斜靠在竖直墙壁上固定不动,两木棍与水平面的倾角均为θ,将一根横截面外径为
如图所示,相距为d的两根直木棍AB和CD相互平行,斜靠在竖直墙壁上固定不动,两木棍与水平面的倾角均为θ,将一根横截面外径为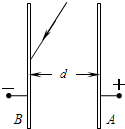 如图所示,相距为d的A、B两平行金属板足够大,板间电压恒为U,有一波长为λ的细激光束照射到B板中央,使B板发生光电效应.已知普朗克恒量为h,金属板B的逸出功为W,电子质量为m,电荷量e,求:
如图所示,相距为d的A、B两平行金属板足够大,板间电压恒为U,有一波长为λ的细激光束照射到B板中央,使B板发生光电效应.已知普朗克恒量为h,金属板B的逸出功为W,电子质量为m,电荷量e,求: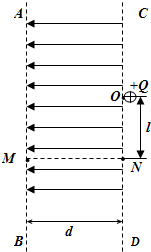 如图所示,相距为d的虚线AB、CD之间存在着水平向左的、场强为E的匀强电场,M、N是平行于电场线的一条直线上的两点,紧靠CD边界的右侧有一O点,与N点相距为l,在O点固定一电荷量为
如图所示,相距为d的虚线AB、CD之间存在着水平向左的、场强为E的匀强电场,M、N是平行于电场线的一条直线上的两点,紧靠CD边界的右侧有一O点,与N点相距为l,在O点固定一电荷量为