题目内容
【题目】如图所示，虚线右侧存在匀强磁场，磁场方向垂直纸面向外，正方形金属框电阻为R，边长是L，自线框从左边界进入磁场时开始计时，在外力作用下由静止开始，以垂直于磁场边界的恒定加速度
进人磁场区域，t1时刻线框全部进入磁场．规定顺时针方向为感应电流I的正方向．外力大小为F，线框中电功率的瞬时值为P，通过导体横截面的电荷量为q，其中P－t图像为抛物线．则这些量随时间变化的关系正确的是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】试题分析：由线框进入磁场中切割磁感线，根据运动学公式可知速度与时间关系；再由法拉第电磁感应定律，可得出产生感应电动势与速度关系；由闭合电路欧姆定律来确定感应电流的大小，并由安培力公式可确定其大小与时间的关系；由牛顿第二定律来确定合力与时间的关系；最后电量、功率的表达式来分别得出各自与时间的关系．
解：A、线框切割磁感线，则有运动速度v=at，产生感应电动势E=BLv，所以产生感应电流
=
，故A错误；
B、对线框受力分析，由牛顿第二定律，则有
解得：
，所以B错误；
C、由功率表达式，
，所以C正确；
D、由电量表达式，则有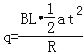
，所以D错误；
故选：C
练习册系列答案
相关题目
