题目内容
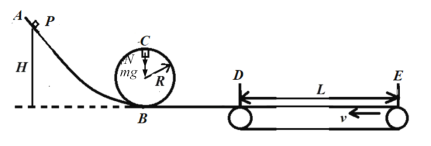
【题目】如图所示,ABCD是光滑轨道,其中竖直圆轨道的半径为R=0.2m,最低点B处入、出口不重合,C点是最高点,BD部分水平,D点与其右侧的水平传送带平滑连接,传送带以速率v=1m/s逆时针匀速转动,水平部分长度L=1m。质量为m=1kg的小物块从轨道上高H=0.6m处的P位置由静止释放,在竖直圆轨道内通过最高点C后经B点进入水平轨道,小物块与传送带间的动摩擦因数μ=0.4,重力加速g取10m/s2。
(1)小物块经过最高点C处时所受轨道的压力N的大小;
(2)小物块在传送带上运动的时间t及小物块与传送带之间摩擦产生的热量Q。

【答案】(1)10N;(2)5.48J
【解析】
(1)设小物块滑到C的速度为vC,从A→C过程由机械能守恒定律得
![]() ①
①
小物块在C处由牛顿第二定律得
![]() ②
②
由①②式解得
![]() ③
③
(2)设小物块进入传送带的速度为v0,加速度大小为a,在传送带上运动的时间为t,到达传送带右端速度为vt;
从P →B过程,由机械能守恒定律
![]() ④
④
从P→E过程,由动能定理
![]() ⑤
⑤
由牛顿第二定律
μmg =ma
得
a=μg=4m/s2⑥
由运动学公式
![]() ⑦
⑦
这段时间内,传送带向左运动的位移
s2=vt2=0.37m ⑧
摩擦产生的热
Q =μmg(L+s2)=5.48J ⑨

练习册系列答案
相关题目