题目内容
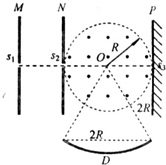 (2012?昆山市模拟)如图所示,两块平行金属板M、N正对着放置,s1、s2分别为M、N板上的小孔,s1、s2、O三点共线,它们的连线垂直M、N,且s2O=R..以O为圆心、R为半径的圆形区域内同时存在磁感应强度为B、方向垂直纸面向外的匀强磁场和电场强度为E的匀强电场.D为收集板,板上各点到O点的距离以及板两端点的距离都为2R,板两端点的连线垂直M、N板.质量为m、电荷量为+q的粒子,经s1进入M、N间的电场后,通过s2进入电磁场区域,然后沿直线打到光屏P上的s3点.粒子在s1处的速度和粒子所受的重力均不计.求:
(2012?昆山市模拟)如图所示,两块平行金属板M、N正对着放置,s1、s2分别为M、N板上的小孔,s1、s2、O三点共线,它们的连线垂直M、N,且s2O=R..以O为圆心、R为半径的圆形区域内同时存在磁感应强度为B、方向垂直纸面向外的匀强磁场和电场强度为E的匀强电场.D为收集板,板上各点到O点的距离以及板两端点的距离都为2R,板两端点的连线垂直M、N板.质量为m、电荷量为+q的粒子,经s1进入M、N间的电场后,通过s2进入电磁场区域,然后沿直线打到光屏P上的s3点.粒子在s1处的速度和粒子所受的重力均不计.求:(1)M、N两板间的电压为U;
(2)撤去圆形区域内的电场后,当M、N间的电压改为U1时,粒子恰好垂直打在收集板D的中点上,求电压U1的值及粒子在磁场中的运动时间t;
(3)撤去圆形区域内的电场后,改变M、N间的电压时,粒子从s2运动到D板经历的时间t会不同,求t的最小值.
分析:(1)粒子在电磁场中沿直线运动,则粒子所受电场力与磁场力合力为零,求出粒子的速度,粒子在MN间做加速运动,由动能定理可以求出加速电场电压.
(2)粒子进入磁场后在洛伦兹力作用下做匀速圆周运动,粒子恰好打在收集板D的中点上时,在磁场中运动
圆弧,轨迹半径等于R,根据牛顿第二定律和动能定理求解M、N间的电压.
(3)粒子从s1到打在D上经历的时间t等于在电场中运动时间、磁场中运动时间和穿出磁场后匀速直线运动的时间之和.M、N间的电压越大,粒子进入磁场时的速度越大,在极板间经历的时间越短,同时在磁场中运动轨迹的半径越大,在磁场中粒子磁场偏转角度越小,运动的时间也会越短,出磁场后匀速运动的时间也越短,故当粒子打在收集板D的右端时,对应时间t最短.根据几何知识求出打在D的右端时轨迹半径,根据前面的结果求出粒子进入磁场时的速度大小,运用运动学公式求出三段时间.
(2)粒子进入磁场后在洛伦兹力作用下做匀速圆周运动,粒子恰好打在收集板D的中点上时,在磁场中运动
| 1 |
| 4 |
(3)粒子从s1到打在D上经历的时间t等于在电场中运动时间、磁场中运动时间和穿出磁场后匀速直线运动的时间之和.M、N间的电压越大,粒子进入磁场时的速度越大,在极板间经历的时间越短,同时在磁场中运动轨迹的半径越大,在磁场中粒子磁场偏转角度越小,运动的时间也会越短,出磁场后匀速运动的时间也越短,故当粒子打在收集板D的右端时,对应时间t最短.根据几何知识求出打在D的右端时轨迹半径,根据前面的结果求出粒子进入磁场时的速度大小,运用运动学公式求出三段时间.
解答:解:(1)正粒子沿直线打到P板上的s3点,可知:qv0B=qE,
粒子在M、N间的加速,由动能定理得:qU=
mv02-0,
解得:U=
;
(2)粒子恰好打在收集板D的中点上,
粒子在磁场中做圆周运动的半径为R由牛顿第二定律可知:qv1B=m
,
由牛顿第二定律得:qU1=
mv12-0,解得:U1=
,
粒子在磁场中做圆周运动的时间为
周期,由T=
,解得t=
;
(3)M、N间的电压越大,粒子进入磁场时的速度越大,
粒子在磁场中运动轨迹的半径越大,在磁场中运动的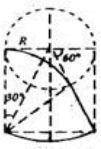 时间也会越短,
时间也会越短,
出磁场后匀速运动的时间也越短,所以当粒子打在收集板D的右端时,对应时间t最短.
根据几何关系可以求得粒子在磁场中运动的半径r=
,
粒子在磁场中运动的时间为t1=
=
,
由牛顿第二定律得:qv2B=m
,
粒子出磁场后做匀速直线运动经历的时间:t2=
=
;
粒子经过s2后打在D上t的最小值tmin=t1+t2=
(π+
);
答:(1)M、N两板间的电压为U=
;
(2)电压U1=
,粒子在磁场中的运动时间t=
;
(3)t的最小值为
(π+
).
粒子在M、N间的加速,由动能定理得:qU=
| 1 |
| 2 |
解得:U=
| mE2 |
| 2qB2 |
(2)粒子恰好打在收集板D的中点上,
粒子在磁场中做圆周运动的半径为R由牛顿第二定律可知:qv1B=m
| ||
| R |
由牛顿第二定律得:qU1=
| 1 |
| 2 |
| qB2R2 |
| 2m |
粒子在磁场中做圆周运动的时间为
| 1 |
| 4 |
| 2πR |
| v1 |
| πm |
| 2qB |
(3)M、N间的电压越大,粒子进入磁场时的速度越大,
粒子在磁场中运动轨迹的半径越大,在磁场中运动的
 时间也会越短,
时间也会越短,出磁场后匀速运动的时间也越短,所以当粒子打在收集板D的右端时,对应时间t最短.
根据几何关系可以求得粒子在磁场中运动的半径r=
| 3R |
粒子在磁场中运动的时间为t1=
| T |
| 6 |
| πm |
| 3qB |
由牛顿第二定律得:qv2B=m
| ||
| r |
粒子出磁场后做匀速直线运动经历的时间:t2=
| T |
| v2 |
| ||
| 3qB |
粒子经过s2后打在D上t的最小值tmin=t1+t2=
| m |
| 3qB |
| 3 |
答:(1)M、N两板间的电压为U=
| mE2 |
| 2qB2 |
(2)电压U1=
| qB2R2 |
| 2m |
| πm |
| 2qB |
(3)t的最小值为
| m |
| 3qB |
| 3 |
点评:本题考查分析和处理粒子在磁场中运动的轨迹问题,难点在于分析时间的最小值,也可以运用极限分析法分析.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 (2012?昆山市模拟)在如图所示电路中,闭合电键 S,当滑动变阻器的滑动触头 P 向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用 I、U1、U2 和 U3 表示,电表示数变化量的大小分别用△I、△U1、△U2 和△U3 表示.下列比值正确的是( )
(2012?昆山市模拟)在如图所示电路中,闭合电键 S,当滑动变阻器的滑动触头 P 向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用 I、U1、U2 和 U3 表示,电表示数变化量的大小分别用△I、△U1、△U2 和△U3 表示.下列比值正确的是( ) (2012?昆山市模拟)(选修模块3-3)
(2012?昆山市模拟)(选修模块3-3) (2012?昆山市模拟)如图所示,两光滑平行导电导轨水平放置于磁感应强度为B的匀强磁场中,磁场与导轨所在平面垂直.已知金属棒ab能沿导轨自由移动,且导轨一端跨接一个定值电阻R,金属棒与导轨电阻均不计.现将金属棒沿导轨以初速度v0开始向右拉动,若保持拉力恒定不变,经过时间t1后金属棒速度变为v,加速度为a1,最终以速度2v做匀速运动.若再使金属棒仍以初速度v0开始,保持拉力的功率不变,经过时间t2后金属棒速度变为v,加速度为a2,最终以速度2v做匀速运动.则( )
(2012?昆山市模拟)如图所示,两光滑平行导电导轨水平放置于磁感应强度为B的匀强磁场中,磁场与导轨所在平面垂直.已知金属棒ab能沿导轨自由移动,且导轨一端跨接一个定值电阻R,金属棒与导轨电阻均不计.现将金属棒沿导轨以初速度v0开始向右拉动,若保持拉力恒定不变,经过时间t1后金属棒速度变为v,加速度为a1,最终以速度2v做匀速运动.若再使金属棒仍以初速度v0开始,保持拉力的功率不变,经过时间t2后金属棒速度变为v,加速度为a2,最终以速度2v做匀速运动.则( )