题目内容
9. 一个小球从静止开始从O点沿斜面以恒定的加速度滚下来,依次通过A、B、C三点,已知AB=18m,BC=30m,小球通过AB、BC所用的时间均为2s,求:
一个小球从静止开始从O点沿斜面以恒定的加速度滚下来,依次通过A、B、C三点,已知AB=18m,BC=30m,小球通过AB、BC所用的时间均为2s,求:(1)小球沿斜面下滑时的加速度大小?
(2)小球通过A点时的速度大小是多少?
(3)OA两点之间的距离为多少?
分析 (1)根据连续相等时间内的位移之差是一恒量求出小球下滑的加速度.
(2)根据某段时间内的平均速度等于中间时刻的瞬时速度求出B点的速度,根据速度时间公式求出A点的速度.
(3)根据速度位移公式求出OA之间的距离.
解答 解:(1)根据△x=aT2得,小球的加速度a=$\frac{△x}{{T}^{2}}=\frac{30-18}{4}m/{s}^{2}=3m/{s}^{2}$.
(2)小球通过B点的速度${v}_{B}=\frac{{x}_{AC}}{2T}=\frac{18+30}{4}m/s=12m/s$,
则A点的速度vA=vB-aT=12-3×2m/s=6m/s.
(3)OA间的距离${x}_{OA}=\frac{{{v}_{A}}^{2}}{2a}=\frac{36}{2×3}m=6m$.
答:(1)小球沿斜面下滑时的加速度大小为3m/s2;
(2)小球通过A点时的速度大小是6m/s;
(3)OA两点之间的距离为6m.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,有时运用推论求解会使问题更加简捷.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
19.如图所示,用绳跨过定滑轮牵引小船,设水的阻力不变,则在小船匀速靠岸的过程中( )


| A. | 绳子的拉力不断增大 | B. | 绳子的拉力不变 | ||
| C. | 船所受浮力增大 | D. | 船所受浮力变大 |
4.某同学身高1.8m,在运动会上他参加跳高比赛,起跳后身体横着越过了1.8m高度的横杆,据此可估算出他起跳时竖直向上的速度大约为(取g=10m/s2)( )
| A. | 4 m/s | B. | 5 m/s | C. | 6 m/s | D. | 8m/s |
14.如图所示的电场中有A、B两点,下述说法正确的是( )


| A. | 点电荷q在A点所受电场力大于在B点所受的电场力 | |
| B. | A点的电势小于B点 | |
| C. | 负电荷在A点的电势能比在B点的电势能小 | |
| D. | 正电荷从B点移到A点时,电场力作正功 |
19.根据打点计时器打出的纸带,我们可以不利用公式计算就能直接得到的物理量是( )
| A. | 加速度 | B. | 位移 | C. | 速度 | D. | 平均速度 |
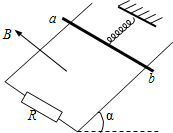 如图所示,光滑的金属导轨间距为L,导轨平面与水平面成α角,导轨下端接有阻值为R的电阻,质量为m的金属细杆ab与绝缘轻质弹簧相连并静止在导轨上,弹簧劲度系数为k,上端固定,弹簧与导轨平面平行,整个装置处在垂直于导轨平面斜向上的匀强磁场中,磁感应强度为B.现给杆一沿轨道向下的初速度v0,杆向下运动至速度为零后,再沿轨道平面向上运动达最大速度,大小为v1,然后减速为零,再沿轨道平面向下运动…一直往复运动到静止(导轨与金属杆的电阻忽略不计).试求:
如图所示,光滑的金属导轨间距为L,导轨平面与水平面成α角,导轨下端接有阻值为R的电阻,质量为m的金属细杆ab与绝缘轻质弹簧相连并静止在导轨上,弹簧劲度系数为k,上端固定,弹簧与导轨平面平行,整个装置处在垂直于导轨平面斜向上的匀强磁场中,磁感应强度为B.现给杆一沿轨道向下的初速度v0,杆向下运动至速度为零后,再沿轨道平面向上运动达最大速度,大小为v1,然后减速为零,再沿轨道平面向下运动…一直往复运动到静止(导轨与金属杆的电阻忽略不计).试求: 一个质量为m=1.0kg的小球,用长为L=2m的细线悬挂于O点,小球在F=10N的水平恒力作用下,从平衡位置P由静止开始运动到Q点,细线偏离竖直方向的角度为θ=30°,则在这一过程中,重力所做的功-10(2-$\sqrt{3}$)J,拉力F做的功10J.
一个质量为m=1.0kg的小球,用长为L=2m的细线悬挂于O点,小球在F=10N的水平恒力作用下,从平衡位置P由静止开始运动到Q点,细线偏离竖直方向的角度为θ=30°,则在这一过程中,重力所做的功-10(2-$\sqrt{3}$)J,拉力F做的功10J. 如图所示的电路中已知电源电动势E=36V,内电阻r=4Ω,R1=30Ω,每盏灯额定功率都是2W,额定电压也相同.当K闭合将电阻箱R2调到R2=16Ω时,两灯都正常发光;当K断开后为使L2仍正常发光,求R2应调到何值?
如图所示的电路中已知电源电动势E=36V,内电阻r=4Ω,R1=30Ω,每盏灯额定功率都是2W,额定电压也相同.当K闭合将电阻箱R2调到R2=16Ω时,两灯都正常发光;当K断开后为使L2仍正常发光,求R2应调到何值?