题目内容
20.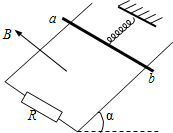 如图所示,光滑的金属导轨间距为L,导轨平面与水平面成α角,导轨下端接有阻值为R的电阻,质量为m的金属细杆ab与绝缘轻质弹簧相连并静止在导轨上,弹簧劲度系数为k,上端固定,弹簧与导轨平面平行,整个装置处在垂直于导轨平面斜向上的匀强磁场中,磁感应强度为B.现给杆一沿轨道向下的初速度v0,杆向下运动至速度为零后,再沿轨道平面向上运动达最大速度,大小为v1,然后减速为零,再沿轨道平面向下运动…一直往复运动到静止(导轨与金属杆的电阻忽略不计).试求:
如图所示,光滑的金属导轨间距为L,导轨平面与水平面成α角,导轨下端接有阻值为R的电阻,质量为m的金属细杆ab与绝缘轻质弹簧相连并静止在导轨上,弹簧劲度系数为k,上端固定,弹簧与导轨平面平行,整个装置处在垂直于导轨平面斜向上的匀强磁场中,磁感应强度为B.现给杆一沿轨道向下的初速度v0,杆向下运动至速度为零后,再沿轨道平面向上运动达最大速度,大小为v1,然后减速为零,再沿轨道平面向下运动…一直往复运动到静止(导轨与金属杆的电阻忽略不计).试求:(1)细杆获得初速度瞬间,通过R的电流大小;
(2)当杆速度为v1时离最初静止时位置的距离L1;
(3)杆由初速度v0开始运动直到最后静止,电阻R上产生的焦耳热Q.
分析 (1)给杆一沿轨道向下的初速度v0,切割磁感线产生的感应电动势为 E=BLv0;根据欧姆定律可求出通过R的电流大小.
(2)由题知道杆沿轨道平面向上运动的最大速度为v1,此时杆所受的合外力为零.分别根据平衡条件和胡克定律求出杆静止时和速度为v1时弹簧伸长的长度,由几何关系可求得L1;
(3)杆由初速度v0开始运动直到最后静止,弹簧的弹性势能不变,杆还静止在开始的位置,动能转化为内能,根据能量守恒求解焦耳热.
解答 解:(1)细杆获得初速度瞬间,产生的感应电动势为:E=BLv0;
根据欧姆定律得:I0=$\frac{E}{R}$
可得通过R的电流大小为:I0=$\frac{BL{v}_{0}}{R}$.
(2)设杆最初静止不动时弹簧伸长x0,则有:kx0=mgsinα
当杆的速度为v1时弹簧伸长x1,由平衡条件得:kx1=mgsinα+BI1L
此时有:I1=$\frac{BL{v}_{1}}{R}$
而 L1=x1-x0
联立解得:L1=$\frac{{B}^{2}{L}^{2}{v}_{1}}{kR}$
(3)杆最后静止时,杆受到重力、导轨的支持力和弹簧的拉力,根据平衡条件和胡克定律可知,弹簧伸长的长度与原来静止时相同,所以杆静止在初始位置,由能量守恒得:
Q=$\frac{1}{2}m{v}_{0}^{2}$
答:
(1)细杆获得初速度瞬间,通过R的电流大小为 $\frac{BL{v}_{0}}{R}$.
(2)当杆速度为v1时离最初静止时位置的距离 L1为 $\frac{{B}^{2}{L}^{2}{v}_{1}}{kR}$.
(3)杆由初速度v0开始运动直到最后静止,电阻R上产生的焦耳为$\frac{1}{2}m{v}_{0}^{2}$.
点评 本题是导体棒在导轨上滑动的类型,正确分析杆的运动状态,确定其受力情况是关键,并能结合能量守恒分析.

 如图所示,一平抛运动的排球,依次飞过三个完全相同的窗户1,2,3,图中曲线为球在空中运行的轨迹,轨迹平面与墙面平行;则下列关于排球经过三个窗户过程判断正确的是( )
如图所示,一平抛运动的排球,依次飞过三个完全相同的窗户1,2,3,图中曲线为球在空中运行的轨迹,轨迹平面与墙面平行;则下列关于排球经过三个窗户过程判断正确的是( )| A. | 经过1号窗的时间最短 | B. | 经过1号窗重力的平均功率最大 | ||
| C. | 经过1号窗的位移最大 | D. | 经过1号窗速度变化的最快 |
| A. | 鸡蛋碰石头,我们看到现象是石头完好,鸡蛋破碎.这说明鸡蛋和石头之间的作用力与反作用力不相等 | |
| B. | 手推车向前运动,手对车的推力与车的重力是作用力与反作用力 | |
| C. | 人拍手时,两手间的相互作用力是作用力与反作用力 | |
| D. | 竖直细线拉一小球悬空静止,线对小球的拉力与小球的重力是一对平衡力 |
| A. | 速度 | B. | 加速度 | C. | 向心力 | D. | 周期 |
| A. | 抽出空气,羽毛和金属片同时落到管底 | |
| B. | 抽出空气,羽毛下落得快 | |
| C. | 不抽出空气,羽毛和金属片同时落到管底 | |
| D. | 不抽出空气,金属片下落得快 |
 如图,当变阻器滑动触头向下滑动时,请讨论电路中各电流表、电压表的示数的变化情况,其中:(填“变大”、“变小”或“不变”)
如图,当变阻器滑动触头向下滑动时,请讨论电路中各电流表、电压表的示数的变化情况,其中:(填“变大”、“变小”或“不变”) 在做“用油膜法估测分子大小”的实验中,所用油酸酒精溶液的浓度为每2000mL溶液中有纯油酸1mL,用注射器测得1mL上述溶液50滴.把l滴该溶液滴入盛水的浅盘里,待液面稳定后,将玻璃板放在浅盘上,用笔在玻璃板上描出油酸的轮廓,再把玻璃板放在坐标纸上,其形状和尺寸如图所示.坐标中正方形方格的边长为1cm,试求:
在做“用油膜法估测分子大小”的实验中,所用油酸酒精溶液的浓度为每2000mL溶液中有纯油酸1mL,用注射器测得1mL上述溶液50滴.把l滴该溶液滴入盛水的浅盘里,待液面稳定后,将玻璃板放在浅盘上,用笔在玻璃板上描出油酸的轮廓,再把玻璃板放在坐标纸上,其形状和尺寸如图所示.坐标中正方形方格的边长为1cm,试求: 一个小球从静止开始从O点沿斜面以恒定的加速度滚下来,依次通过A、B、C三点,已知AB=18m,BC=30m,小球通过AB、BC所用的时间均为2s,求:
一个小球从静止开始从O点沿斜面以恒定的加速度滚下来,依次通过A、B、C三点,已知AB=18m,BC=30m,小球通过AB、BC所用的时间均为2s,求: