题目内容
5.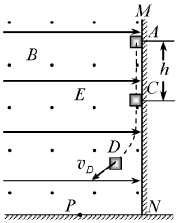 如图,绝缘粗糙的竖直平面MN左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为E,磁场方向垂直纸面向外,磁感应强度大小为B.一质量为m,电荷量为q的带正电的小滑块从A点由静止开始沿MN下滑,到达C点时离开MN做曲线运动.A、C两点间距离为h,重力加速度为g.
如图,绝缘粗糙的竖直平面MN左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为E,磁场方向垂直纸面向外,磁感应强度大小为B.一质量为m,电荷量为q的带正电的小滑块从A点由静止开始沿MN下滑,到达C点时离开MN做曲线运动.A、C两点间距离为h,重力加速度为g.(1)求小滑块运动到C点时的速度大小vc;
(2)求小滑块从A点运动到C点过程中克服摩擦力做的功Wf;
(3)若D点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置,当小滑块运动到D点时撤去磁场,此后小滑块继续运动到水平地面上的P点.已知小滑块在D点时的速度大小为vD,从D点运动到P点的时间为t,求小滑块运动到P点时速度的大小vp.
分析 (1)小滑块到达C点时离开MN,此时与MN间的作用力为零,对小滑块受力分析计算此时的速度的大小;
(2)由动能定理直接计算摩擦力做的功Wf;
(3)撤去磁场后小滑块将做类平抛运动,根据分运动计算最后的合速度的大小;
解答 解:(1)小滑块沿MN运动过程,水平方向受力满足
qvB+N=qE
小滑块在C点离开MN时
N=0
解得 vc=$\frac{E}{B}$
(2)由动能定理
mgh-Wf=$\frac{1}{2}m{v}_{c}^{2}$-0
解得 Wf=mgh-$\frac{m{E}^{2}}{2{B}^{2}}$
(3)如图,
小滑块速度最大时,速度方向与电场力、重力的合力方向垂直,
撤去磁场后小滑块将做类平抛运动,等效加速度为g′,
g′=$\sqrt{(\frac{qE}{m})^{2}+{g}^{2}}$
且${v}_{p}^{2}={v}_{D}^{2}+g{′}^{2}{t}^{2}$
解得 ${v}_{p}=\sqrt{{v}_{D}^{2}+[{(\frac{qE}{m})}^{2}+{g}^{2}]{t}^{2}}$
答:(1)小滑块运动到C点时的速度大小vc为$\frac{E}{B}$;
(2)小滑块从A点运动到C点过程中克服摩擦力做的功Wf为mgh-$\frac{m{E}^{2}}{2{B}^{2}}$;
(3)小滑块运动到P点时速度的大小vp为$\sqrt{{v}_{D}^{2}+[{(\frac{qE}{m})}^{2}+{g}^{2}]{t}^{2}}$.
点评 解决本题的关键是分析清楚小滑块的运动过程,在与MN分离时,小滑块与MN间的作用力为零,在撤去磁场后小滑块将做类平抛运动,根据滑块的不同的运动过程逐步求解即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.图甲为一列简谐横波在某一时刻的波形图,a、b两质点的横坐标分别为xa=2m和xb=6m,图乙为质点b从该时刻开始计时的振动图象,下列说法正确的是( )
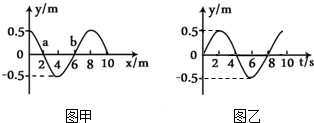

| A. | 该波沿+x方向传播,波速为1m/s | B. | 质点a经4s振动的路程为4m | ||
| C. | 此时刻质点a的速度沿+y方向 | D. | 质点a在t=2s时速度为零 |
10. 如图所示,用两根长度相同的绝缘细线把一个质量为0.1kg的小球A悬挂在水平板的M、N两点,A上带有Q=3.0×10-6C的正电荷,两线夹角为120°,两线上的拉力大小分别为F1和F2,A的正下方0.3m处放有一带等量异种电荷的小球B,B与绝缘支架的总质量为0.2kg(重力加速度取g=10m/s2;静电力常量k=9.0×109N•m2/C2,A、B球可视为点电荷),则( )
如图所示,用两根长度相同的绝缘细线把一个质量为0.1kg的小球A悬挂在水平板的M、N两点,A上带有Q=3.0×10-6C的正电荷,两线夹角为120°,两线上的拉力大小分别为F1和F2,A的正下方0.3m处放有一带等量异种电荷的小球B,B与绝缘支架的总质量为0.2kg(重力加速度取g=10m/s2;静电力常量k=9.0×109N•m2/C2,A、B球可视为点电荷),则( )
 如图所示,用两根长度相同的绝缘细线把一个质量为0.1kg的小球A悬挂在水平板的M、N两点,A上带有Q=3.0×10-6C的正电荷,两线夹角为120°,两线上的拉力大小分别为F1和F2,A的正下方0.3m处放有一带等量异种电荷的小球B,B与绝缘支架的总质量为0.2kg(重力加速度取g=10m/s2;静电力常量k=9.0×109N•m2/C2,A、B球可视为点电荷),则( )
如图所示,用两根长度相同的绝缘细线把一个质量为0.1kg的小球A悬挂在水平板的M、N两点,A上带有Q=3.0×10-6C的正电荷,两线夹角为120°,两线上的拉力大小分别为F1和F2,A的正下方0.3m处放有一带等量异种电荷的小球B,B与绝缘支架的总质量为0.2kg(重力加速度取g=10m/s2;静电力常量k=9.0×109N•m2/C2,A、B球可视为点电荷),则( )| A. | 支架对地面的压力大小为2.0N | |
| B. | 两线上的拉力大小F1=F2=1.9N | |
| C. | 将B水平右移,使M、A、B在同一直线上,此时两线上的拉力大小F1=1.225N,F2=1.0N | |
| D. | 将B移到无穷远处,两线上的拉力大小F1=F2=0.866N |
14. 如图所示,用力F推A,使叠放在一起的A、B一起沿桌面向右匀速运动,直到木板翻离桌面,则该过程中( )
如图所示,用力F推A,使叠放在一起的A、B一起沿桌面向右匀速运动,直到木板翻离桌面,则该过程中( )
 如图所示,用力F推A,使叠放在一起的A、B一起沿桌面向右匀速运动,直到木板翻离桌面,则该过程中( )
如图所示,用力F推A,使叠放在一起的A、B一起沿桌面向右匀速运动,直到木板翻离桌面,则该过程中( )| A. | A、B间一定有摩擦力 | |
| B. | B与桌面间一定无摩擦力 | |
| C. | 力F逐渐变小 | |
| D. | 若用力F推B,使A、B一起沿桌面向右匀速运动,则F变大 |
4.下列有关牛顿运动定律的说法,其中正确的是( )
| A. | 惯性就是物体保持静止状态的性质 | |
| B. | 一对作用力和反作用力的作用效果总相同 | |
| C. | 物体运动状态改变的难易程度与物体的速度有关 | |
| D. | 力的国际制单位“牛顿”是根据牛顿第二定律定义的 |
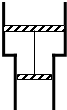 如图,一固定的竖直汽缸由一大一小两个同轴圆筒组成,两圆筒中各有一个活塞,已知大活塞的质量为m1=2.50kg,横截面积为s1=80.0cm2,小活塞的质量为m2=1.50kg,横截面积为s2=40.0cm2,两活塞用刚性轻杆连接,间距保持为l=40.0cm,汽缸外大气的压强为p=1.00×105Pa,温度为T=303K,初始时大活塞与大圆筒底部相距$\frac{l}{2}$,两活塞间封闭气体的温度为T1=495K,现汽缸内气体温度缓慢下降,活塞缓慢下移,忽略两活塞与汽缸壁之间的摩擦,重力加速度大小g取10m/s2,求:
如图,一固定的竖直汽缸由一大一小两个同轴圆筒组成,两圆筒中各有一个活塞,已知大活塞的质量为m1=2.50kg,横截面积为s1=80.0cm2,小活塞的质量为m2=1.50kg,横截面积为s2=40.0cm2,两活塞用刚性轻杆连接,间距保持为l=40.0cm,汽缸外大气的压强为p=1.00×105Pa,温度为T=303K,初始时大活塞与大圆筒底部相距$\frac{l}{2}$,两活塞间封闭气体的温度为T1=495K,现汽缸内气体温度缓慢下降,活塞缓慢下移,忽略两活塞与汽缸壁之间的摩擦,重力加速度大小g取10m/s2,求: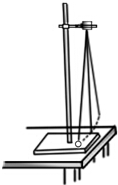 某同学利用单摆测量重力加速度.
某同学利用单摆测量重力加速度. 如图所示,N=50匝的矩形线圈abcd,ab边长l1=20cm,ad边长l2=25cm,放在磁感强度B=0.4T的匀强磁场中,外力使线圈绕垂直于磁感线且通过线圈中线的OO′轴以n=3000r/min的转速匀速转动,线圈电阻r=1Ω,外电路电阻R=9Ω,t=0时,线圈平面与磁感线平行,ab边正转出纸外、cd边转入纸里.
如图所示,N=50匝的矩形线圈abcd,ab边长l1=20cm,ad边长l2=25cm,放在磁感强度B=0.4T的匀强磁场中,外力使线圈绕垂直于磁感线且通过线圈中线的OO′轴以n=3000r/min的转速匀速转动,线圈电阻r=1Ω,外电路电阻R=9Ω,t=0时,线圈平面与磁感线平行,ab边正转出纸外、cd边转入纸里.