题目内容
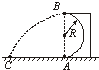
英国特技演员史蒂夫?特鲁加里亚曾飞车挑战世界最大环形车道.如图所示,环形车道竖直放置,半径为6m,若汽车在车道上以12m/s恒定的速率运动,演员与汽车的总质量为1000kg,重力加速度g取10m/s2,则( )

| A.汽车通过最低点时,演员处于超重状态 |
| B.汽车通过最高点时对环形车道的压力为1.4×104N |
| C.若要挑战成功,汽车在最高点的速率不可能低于12m/s |
| D.汽车在环形车道上的角速度为1rad/s |

A、汽车通过最低点时,加速度方向竖直向上,演员处于超重状态.故A正确.
B、根据牛顿第二定律得,N+mg=m
,解得N=m
-mg=1000×
-10000N=14000N.故B正确.
C、要想通过最高点,临界情况是轨道对汽车的压力为零,根据牛顿第二定律得,mg=m
,解得v′=
=
m/s=2
m/s.即最小速度为2
m/s.故C错误.
D、汽车在环形车道上的角速度ω=
=
rad/s=2rad/s.故D错误.
故选:AB.
B、根据牛顿第二定律得,N+mg=m
| v2 |
| R |
| v2 |
| R |
| 144 |
| 6 |
C、要想通过最高点,临界情况是轨道对汽车的压力为零,根据牛顿第二定律得,mg=m
| v′2 |
| R |
| gR |
| 10×6 |
| 15 |
| 15 |
D、汽车在环形车道上的角速度ω=
| v |
| R |
| 12 |
| 6 |
故选:AB.

练习册系列答案
相关题目