题目内容
10.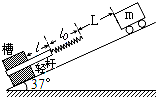 倾角为37°的光滑斜面上固定一个槽,劲度系数k=20N/m、原长l0=0.6m的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.3m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小Ff=6N,杆与槽之间的最大静摩擦力等于滑动摩擦力.质量m=1kg的小车从距弹簧上端L=0.6m处由静止释放沿斜面向下运动.已知弹性势能EP=$\frac{1}{2}k{x^2}$,式中x为弹簧的形变量.g取10m/s2,sin37°=0.6.若只考虑沿斜面向下的运动过程,关于小车和杆的运动情况,下列说法正确的是( )
倾角为37°的光滑斜面上固定一个槽,劲度系数k=20N/m、原长l0=0.6m的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.3m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小Ff=6N,杆与槽之间的最大静摩擦力等于滑动摩擦力.质量m=1kg的小车从距弹簧上端L=0.6m处由静止释放沿斜面向下运动.已知弹性势能EP=$\frac{1}{2}k{x^2}$,式中x为弹簧的形变量.g取10m/s2,sin37°=0.6.若只考虑沿斜面向下的运动过程,关于小车和杆的运动情况,下列说法正确的是( )| A. | 小车先做匀加速运动,后做加速度逐渐减小的变加速运动 | |
| B. | 在杆滑动之前,小车的机械能守恒 | |
| C. | 杆在完全进入槽内前瞬间速度为3m/s | |
| D. | 杆在完全进入槽内前瞬间弹性势能大于0.9J |
分析 对小车在碰撞弹簧前后受力分析,根据力判断其运动情况,根据机械能守恒定律的条件判断小车的机械能是否守恒,当弹簧和杆整体受到的力等于静摩擦力的时候,轻杆开始滑动,根据平衡条件求出弹簧的压缩量,根据能量守恒求出此时的速度.
解答 解:A、一开始小车受恒力向下做匀加速运动,后来接触到弹簧,合力逐渐变小,于是做加速度逐渐变小的变加速运动,最后受到弹簧轻杆的力和重力沿斜面向下的分力平衡,于是做匀速直线运动,故A错误;
B、一开始小车向下做匀加速运动,只有重力做功,机械能守恒,与弹簧接触后,小车与弹簧组成的系统机械能守恒,但小车的机械能不守恒,故B错误;
C、当弹簧和杆整体受到的力等于静摩擦力的时候,轻杆开始滑动,此时由平衡得:弹簧压缩量有公式Ff=k△x解得:△x=0.3m,当弹簧的压缩量为0.3m的时候,弹簧的弹力和小车在斜面上的分力相等,此时整个系统开始做匀速运动,设此速度为v,从小车开始运动到做匀速运动,有能量守恒得:$mg(L+△x)sinθ=\frac{1}{2}m{v}^{2}+\frac{1}{2}k△{x}^{2}$,
代入数据求得:v=3m/s,故C正确;
D、小车刚匀速运动时,弹簧的弹性势能为:EP=$\frac{1}{2}k{△x}^{2}=\frac{1}{2}×20×0.09=0.9J$,此后小车和弹簧都做匀速运动,弹簧的压缩量不变,则弹性势能一直为0.9J,故D错误.
故选:C.
点评 本题的关键是分清小车的运动过程,特别是接触弹簧后的情况,弹力突变导致静摩擦力也跟着变,找出最后运动状态后利用能的观点即可求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.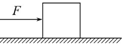 如图所示,在F的作用下,质量为m的物体做匀速运动,已知物体与地面间的动摩擦因数为μ,则物体与地面间的摩擦力大小有以下四种说法,其中正确的是( )
如图所示,在F的作用下,质量为m的物体做匀速运动,已知物体与地面间的动摩擦因数为μ,则物体与地面间的摩擦力大小有以下四种说法,其中正确的是( )
 如图所示,在F的作用下,质量为m的物体做匀速运动,已知物体与地面间的动摩擦因数为μ,则物体与地面间的摩擦力大小有以下四种说法,其中正确的是( )
如图所示,在F的作用下,质量为m的物体做匀速运动,已知物体与地面间的动摩擦因数为μ,则物体与地面间的摩擦力大小有以下四种说法,其中正确的是( )| A. | f=0 | B. | f=μmg | C. | f=F | D. | f=μmg-F |
15.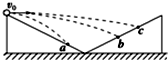 如图所示,横截面为直角三角形的两个相同斜面紧靠在一起,固定在水平面上,它们的竖直边长都是底边长的一半.小球从左边斜面的顶点以不同的初速度向右水平抛出,最后落在斜面上.其中有三次的落点分别是a、b、c.下列判断正确的是( )
如图所示,横截面为直角三角形的两个相同斜面紧靠在一起,固定在水平面上,它们的竖直边长都是底边长的一半.小球从左边斜面的顶点以不同的初速度向右水平抛出,最后落在斜面上.其中有三次的落点分别是a、b、c.下列判断正确的是( )
 如图所示,横截面为直角三角形的两个相同斜面紧靠在一起,固定在水平面上,它们的竖直边长都是底边长的一半.小球从左边斜面的顶点以不同的初速度向右水平抛出,最后落在斜面上.其中有三次的落点分别是a、b、c.下列判断正确的是( )
如图所示,横截面为直角三角形的两个相同斜面紧靠在一起,固定在水平面上,它们的竖直边长都是底边长的一半.小球从左边斜面的顶点以不同的初速度向右水平抛出,最后落在斜面上.其中有三次的落点分别是a、b、c.下列判断正确的是( )| A. | 图中三小球比较,落在a点的小球飞行时间最短 | |
| B. | 小球落在a点的飞行时间与初速度v0成正比 | |
| C. | 图中三小球比较,落在c点的小球飞行过程速度变化最小 | |
| D. | 小球可能垂直落到右边斜面上的b点 |
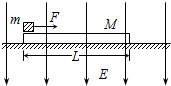 质量为m=1.0kg、带电量q=2.5×10-4C的小滑块(可视为质点)放在质量为M=2.0kg的绝缘长木板的左端,木板放在光滑水平面上,滑块与木板之间的动摩擦因数为μ=0.2,木板长L=1.5m.开始时两者都处于静止状态,所在空间加有一个方向竖直向下电场强度为E=4.0×104N/C的匀强电场,如图所示.取g=10m/s2,试求:
质量为m=1.0kg、带电量q=2.5×10-4C的小滑块(可视为质点)放在质量为M=2.0kg的绝缘长木板的左端,木板放在光滑水平面上,滑块与木板之间的动摩擦因数为μ=0.2,木板长L=1.5m.开始时两者都处于静止状态,所在空间加有一个方向竖直向下电场强度为E=4.0×104N/C的匀强电场,如图所示.取g=10m/s2,试求:
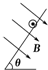
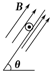
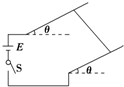 如图所示,光滑的平行导轨与电源连接后,与水平方向成θ角倾斜放置,导轨上放一个质量为m的金属导体棒.当S闭合后,在棒所在区域内加一个合适的匀强磁场,可以使导体棒静止平衡,下面四个图中分别加了不同方向的磁场,其中可能平衡的是( )
如图所示,光滑的平行导轨与电源连接后,与水平方向成θ角倾斜放置,导轨上放一个质量为m的金属导体棒.当S闭合后,在棒所在区域内加一个合适的匀强磁场,可以使导体棒静止平衡,下面四个图中分别加了不同方向的磁场,其中可能平衡的是( )