题目内容
2. 如图所示,将一长度为L=0.8m的轻质细线一端系一质量m=1kg的小球,另一端固定于天花板上,小球以一定大小的速度在水平面做匀速圆周运动,g=10m/s2.求:
如图所示,将一长度为L=0.8m的轻质细线一端系一质量m=1kg的小球,另一端固定于天花板上,小球以一定大小的速度在水平面做匀速圆周运动,g=10m/s2.求:(1)当细线与竖直方向的夹角θ=60°时,细线上的拉力F大小和小球做匀速圆周运动的角速度大小;
(2)如果小球在水平面内做圆周运动过程中,始终受到空气阻力的作用,细线与竖直 方向的夹角θ会缓慢减小,则从细线与竖直方向的夹角θ=60°做圆周运动到小球最终静止的过程中,小球克服空气阻力做的功为多大?
分析 (1)对小球受力分析,受重力和拉力,小球做匀速圆周运动,合力提供向心力,根据几何关系结合牛顿第二定律列式求解;
(2)先求出细线与竖直方向的夹角θ=60°时小球的速度,进而求出此时的动能,再对小球运动到静止的过程,根据动能定理列式求解.
解答 解:(1)当θ=60°时,细线上的作用力F=$\frac{mg}{cos60°}=\frac{10}{\frac{1}{2}}=20N$,
小球在水平面内做匀速圆周运动,合外力提供向心力,则有:
mgtan60°=mω2Lsin60°
解得:$ω=\sqrt{\frac{g}{Lcos60°}}=5rad/s$
(2)根据合外力提供向心力得:
$mgtan60°=m\frac{{v}^{2}}{Lsin60°}$
动能${E}_{K}=\frac{1}{2}m{v}^{2}$
联立解得EK=6J
根据动能定理得:
-W+mgL(1-cos60°)=0-EK
解得:W=10J
答:(1)当细线与竖直方向的夹角θ=60°时,细线上的拉力F大小为20N,小球做匀速圆周运动的角速度大小为5rad/s;
(2)小球克服空气阻力做的功为10J.
点评 本题是圆锥摆问题,关键要正确分析受力,搞清小球做圆周运动向心力的来源:重力和拉力的合力,要注意小球圆周运动的半径不是L,而是Lsinθ.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
14.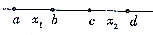 2014年8月3日云南省鲁甸发生6.5级地震,全国各地纷纷前往支援.一辆汽车正在前往救援的平直公路上匀速行驶,由于前方道路遭到严重破坏,司机采取紧急刹车做匀减速运动,依次经过a、b、c、d四点,如图所示,已知通过ab、bc和cd位移的时间之比为1:2:3,ab和cd距离分别为x1和x2,则bc段的距离为( )
2014年8月3日云南省鲁甸发生6.5级地震,全国各地纷纷前往支援.一辆汽车正在前往救援的平直公路上匀速行驶,由于前方道路遭到严重破坏,司机采取紧急刹车做匀减速运动,依次经过a、b、c、d四点,如图所示,已知通过ab、bc和cd位移的时间之比为1:2:3,ab和cd距离分别为x1和x2,则bc段的距离为( )
 2014年8月3日云南省鲁甸发生6.5级地震,全国各地纷纷前往支援.一辆汽车正在前往救援的平直公路上匀速行驶,由于前方道路遭到严重破坏,司机采取紧急刹车做匀减速运动,依次经过a、b、c、d四点,如图所示,已知通过ab、bc和cd位移的时间之比为1:2:3,ab和cd距离分别为x1和x2,则bc段的距离为( )
2014年8月3日云南省鲁甸发生6.5级地震,全国各地纷纷前往支援.一辆汽车正在前往救援的平直公路上匀速行驶,由于前方道路遭到严重破坏,司机采取紧急刹车做匀减速运动,依次经过a、b、c、d四点,如图所示,已知通过ab、bc和cd位移的时间之比为1:2:3,ab和cd距离分别为x1和x2,则bc段的距离为( )| A. | $\frac{{x}_{1}+{x}_{2}}{2}$ | B. | $\frac{2{x}_{1}{x}_{2}}{{x}_{1}+{x}_{2}}$ | C. | $\frac{3{x}_{1}+4{x}_{2}}{4}$ | D. | $\frac{5{x}_{1}+{x}_{2}}{4}$ |
10.作用在同一个物体上的两个共点力,一个是10N,一个是3N,它们的合力可能是( )
| A. | 0 | B. | 3N | C. | 5N | D. | 10N |
 在绝缘水平面上,A、B两金属块的质量都为m,最初都静止,相距为s,A带电量为+q,B不带电.A与水平面间无摩擦.当突然加上水平向右的足够大的匀强电场E后.A向右运动,和B相碰,并且粘连到一起.设B与水平面间的动摩擦力为3qE.
在绝缘水平面上,A、B两金属块的质量都为m,最初都静止,相距为s,A带电量为+q,B不带电.A与水平面间无摩擦.当突然加上水平向右的足够大的匀强电场E后.A向右运动,和B相碰,并且粘连到一起.设B与水平面间的动摩擦力为3qE.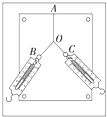 在“探究力的平行四边形定则”的实验中,用图钉把橡皮条的一端固定在板上的A点,在橡皮条的另一端拴上两条细绳,细绳另一端系着绳套B、C(用来连接弹簧测力计).其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.
在“探究力的平行四边形定则”的实验中,用图钉把橡皮条的一端固定在板上的A点,在橡皮条的另一端拴上两条细绳,细绳另一端系着绳套B、C(用来连接弹簧测力计).其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.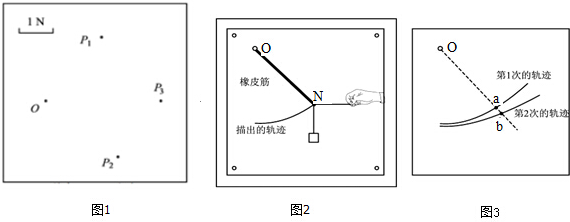

 如图所示,在某环境下用截面积为0.2m2的轻质绝热活塞,将一定质量的理想气体封闭在圆柱形汽缸内,活塞与汽缸之间无摩擦,a状态是汽缸放在冰水混合物中气体达到的平衡状态,活塞离汽缸底部高度为0.6m,b状态是汽缸从容器中移除后达到的平衡状态,活塞离汽缸底部的高度为0.7m,设该环境中大气压强始终保持1.0×105Pa.
如图所示,在某环境下用截面积为0.2m2的轻质绝热活塞,将一定质量的理想气体封闭在圆柱形汽缸内,活塞与汽缸之间无摩擦,a状态是汽缸放在冰水混合物中气体达到的平衡状态,活塞离汽缸底部高度为0.6m,b状态是汽缸从容器中移除后达到的平衡状态,活塞离汽缸底部的高度为0.7m,设该环境中大气压强始终保持1.0×105Pa. 如图所示,小木箱abcd的质量M=0.18kg,高L=0.2m,其顶部离挡板E的距离h=0.8m,在木箱内放有一个质量为m=0.02kg的小物体P(其高度很小,可以忽略不计),设想对木箱施加一个竖直向上的恒力F的作用使其由静止开始向上做匀加速运动,木箱和挡板碰后立即停在挡板处,为使小物体P不会和木箱顶部ad相碰,求恒力F的取值范围.(g=10m/s2,不计空气阻力)
如图所示,小木箱abcd的质量M=0.18kg,高L=0.2m,其顶部离挡板E的距离h=0.8m,在木箱内放有一个质量为m=0.02kg的小物体P(其高度很小,可以忽略不计),设想对木箱施加一个竖直向上的恒力F的作用使其由静止开始向上做匀加速运动,木箱和挡板碰后立即停在挡板处,为使小物体P不会和木箱顶部ad相碰,求恒力F的取值范围.(g=10m/s2,不计空气阻力)