题目内容
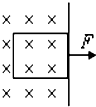 如图所示,从匀强磁场中把不发生形变的矩形线圈匀速拉出磁场区,如果两次拉出的速度之比为1:2,则两次线圈发热之比Q1:Q2=
如图所示,从匀强磁场中把不发生形变的矩形线圈匀速拉出磁场区,如果两次拉出的速度之比为1:2,则两次线圈发热之比Q1:Q2=分析:在拉力作用下,矩形线圈以不同速度被匀速拉出,拉力做功等于克服安培力做功,等于产生的焦耳热.根据法拉第电磁感应定律、欧姆定律、安培力公式列式,再进行求解.
解答:解:设任意线圈左右两边边长为l,上下两边边长为l′,整个线圈的电阻为R,磁场的磁感应强度为B.
拉出线圈时产生的感应电动势为:E=Blv
感应电流为:I=
线圈所受的安培力为:F=BIl=
拉力做功为:W=Fl′=
?l′
根据功能关系得知,拉力做功等于克服安培力做功,等于产生的焦耳热,则得线圈将产生的热量 Q=W
可知Q∝v,则得:Q1:Q2=1:2.
通过导线的电荷量为:q=It=
t=
t
而vt=l′
则得:q=
可知,q与线框移动速度无关,所以通过导线横截面的电荷量 q1:q2=1:1.
故答案为:1:2,1:1
拉出线圈时产生的感应电动势为:E=Blv
感应电流为:I=
| E |
| R |
线圈所受的安培力为:F=BIl=
| B2l2v |
| R |
拉力做功为:W=Fl′=
| B2l2v |
| R |
根据功能关系得知,拉力做功等于克服安培力做功,等于产生的焦耳热,则得线圈将产生的热量 Q=W
可知Q∝v,则得:Q1:Q2=1:2.
通过导线的电荷量为:q=It=
| E |
| R |
| Blv |
| R |
而vt=l′
则得:q=
| Bll′ |
| R |
可知,q与线框移动速度无关,所以通过导线横截面的电荷量 q1:q2=1:1.
故答案为:1:2,1:1
点评:本题中推导安培力的表达式F=
和感应电量表达式q=
是关键,这两个结论是电磁感应问题常用的经验公式,最好记住.
| B2l2v |
| R |
| Bll′ |
| R |

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
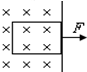 如图所示,从匀强磁场中把不发生形变的矩形线圈匀速拉出磁场区,如果两次拉出的速度之比为1:2,则两次线圈所受外力大小之比F1:F2、线圈发热之比Q1:Q2( )
如图所示,从匀强磁场中把不发生形变的矩形线圈匀速拉出磁场区,如果两次拉出的速度之比为1:2,则两次线圈所受外力大小之比F1:F2、线圈发热之比Q1:Q2( )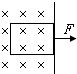 如图所示,从匀强磁场中把不发生形变的矩形线圈匀速拉出磁场区,如果两次拉出的速度之比为1:2,则两次线圈所受外力大小之比F1:F2、线圈发热之比Q1:Q2、通过线圈截面的电量q1:q2之比分别为( )
如图所示,从匀强磁场中把不发生形变的矩形线圈匀速拉出磁场区,如果两次拉出的速度之比为1:2,则两次线圈所受外力大小之比F1:F2、线圈发热之比Q1:Q2、通过线圈截面的电量q1:q2之比分别为( )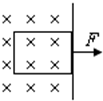 如图所示,从匀强磁场中用外力把一矩形线圈匀速拉出磁场区域.如果两次拉出的速度之比v1:v2=1:2,则在将线圈拉出磁场区域的过程中,两次所用的外力大小之比F1:F2=
如图所示,从匀强磁场中用外力把一矩形线圈匀速拉出磁场区域.如果两次拉出的速度之比v1:v2=1:2,则在将线圈拉出磁场区域的过程中,两次所用的外力大小之比F1:F2=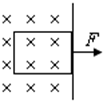 如图所示,从匀强磁场中用外力把一矩形线圈匀速拉出磁场区 域.如果两次拉出的速度之比v1:v2=1:2,则在将线圈拉出磁场区域的过程中,两次所用的外力大小之比F1:F2=
如图所示,从匀强磁场中用外力把一矩形线圈匀速拉出磁场区 域.如果两次拉出的速度之比v1:v2=1:2,则在将线圈拉出磁场区域的过程中,两次所用的外力大小之比F1:F2=