题目内容
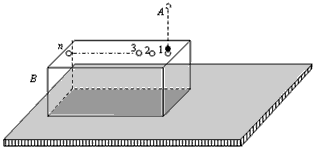
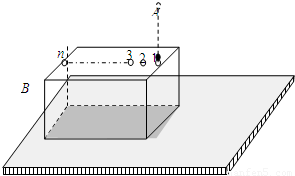 如图所示,A为位于一定高度处的质量为m=1×10-5kg、带电荷量为q=+1×10-6C的微粒,B为位于水平地面上的质量为M的用特殊材料制成的长方形空心盒子,盒子与地面间的动摩擦因数μ=0.2,盒内存在着竖直向上的匀强电场,场强大小E=1×103N/C,盒外存在着竖直向下的匀强电场,场强大小也为E,盒的上表面开有一系列略大于微粒的小孔,孔间距满足一定的关系,使得微粒进出盒子的过程中始终不与盒子接触.当微粒A以1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v1=0.4m/s的速度向右滑行.设盒子足够长,取重力加速度g=10m/s2,不计微粒的重力,微粒恰能顺次从各个小孔进出盒子.试求:
如图所示,A为位于一定高度处的质量为m=1×10-5kg、带电荷量为q=+1×10-6C的微粒,B为位于水平地面上的质量为M的用特殊材料制成的长方形空心盒子,盒子与地面间的动摩擦因数μ=0.2,盒内存在着竖直向上的匀强电场,场强大小E=1×103N/C,盒外存在着竖直向下的匀强电场,场强大小也为E,盒的上表面开有一系列略大于微粒的小孔,孔间距满足一定的关系,使得微粒进出盒子的过程中始终不与盒子接触.当微粒A以1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v1=0.4m/s的速度向右滑行.设盒子足够长,取重力加速度g=10m/s2,不计微粒的重力,微粒恰能顺次从各个小孔进出盒子.试求:(1)从微粒第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程;
(2)微粒A从第一次进入盒子到第二次进入盒子所经历的时间;
(3)盒子上至少要开多少个小孔,才能保证微粒始终不与盒子接触.
【答案】分析:(1)盒子做匀减速运动,求出盒子的加速度,根据匀变速直线运动位移速度公式即可求解;
(2)小球A从第一次进入盒子到第二次进入盒子所经历的时间分为两部分,A在盒子内运动时运动牛顿第二定律求出加速度,再用运动学基本公式求出时间,A在盒子外运动的时间根据运动学基本公式即可求得,时间之和即为经历的总时间;
(3)分别求出小球在盒内和盒外时的盒子的加速度,进而求出小球运动一个周期盒子减少的速度,再求出从小球第一次进入盒子到盒子停下,小球运动的周期数n,要保证小球始终不与盒子相碰,盒子上的小孔数至少为2n+1个.
解答:解:(1)微粒在盒子内、外运动时,盒子的加速度a′=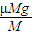 =μg=0.2×10 m/s2=2 m/s2,盒子全过程做匀减速直线运动,所以通过的总路程是:
=μg=0.2×10 m/s2=2 m/s2,盒子全过程做匀减速直线运动,所以通过的总路程是:
(2)A在盒子内运动时,qE=ma方向以向上为正方向
由以上得a=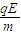 =
=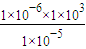 m/s2=1×102 m/s2
m/s2=1×102 m/s2
A在盒子外运动时,qE=ma则a=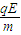 =1×102 m/s2 方向向下
=1×102 m/s2 方向向下
A在盒子内运动的时间t1=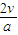 =
=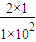 s=2×10-2s,同理A在盒子外运动的时间t2=2×10-2s,A从第一次进入盒子到第二次进入盒子的时间t=t1+t2=4×10-2s.
s=2×10-2s,同理A在盒子外运动的时间t2=2×10-2s,A从第一次进入盒子到第二次进入盒子的时间t=t1+t2=4×10-2s.
(3)微粒运动一个周期盒子减少的速度为△v=a′(t1+t2)=2×(0.02+0.02)=0.08m/s
从小球第一次进入盒子到盒子停下,微粒球运动的周期数为n=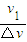 =
=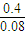 =5,故要保证小球始终不与盒子相碰,盒子上的小孔数至少为2n+1个,即11个.
=5,故要保证小球始终不与盒子相碰,盒子上的小孔数至少为2n+1个,即11个.
答:(1)从微粒第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程为0.04m;
(2)微粒A从第一次进入盒子到第二次进入盒子所经历的时间为4×10-2s;
(3)盒子上至少要开11个小孔,才能保证微粒始终不与盒子接触.
点评:该题是较为复杂的往复运动,要求同学们能正确分析每个过程的受力情况,求出加速度、时间和位移,要求较高,难度适中.
(2)小球A从第一次进入盒子到第二次进入盒子所经历的时间分为两部分,A在盒子内运动时运动牛顿第二定律求出加速度,再用运动学基本公式求出时间,A在盒子外运动的时间根据运动学基本公式即可求得,时间之和即为经历的总时间;
(3)分别求出小球在盒内和盒外时的盒子的加速度,进而求出小球运动一个周期盒子减少的速度,再求出从小球第一次进入盒子到盒子停下,小球运动的周期数n,要保证小球始终不与盒子相碰,盒子上的小孔数至少为2n+1个.
解答:解:(1)微粒在盒子内、外运动时,盒子的加速度a′=
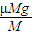 =μg=0.2×10 m/s2=2 m/s2,盒子全过程做匀减速直线运动,所以通过的总路程是:
=μg=0.2×10 m/s2=2 m/s2,盒子全过程做匀减速直线运动,所以通过的总路程是:
(2)A在盒子内运动时,qE=ma方向以向上为正方向
由以上得a=
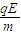 =
=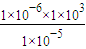 m/s2=1×102 m/s2
m/s2=1×102 m/s2A在盒子外运动时,qE=ma则a=
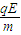 =1×102 m/s2 方向向下
=1×102 m/s2 方向向下A在盒子内运动的时间t1=
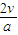 =
=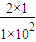 s=2×10-2s,同理A在盒子外运动的时间t2=2×10-2s,A从第一次进入盒子到第二次进入盒子的时间t=t1+t2=4×10-2s.
s=2×10-2s,同理A在盒子外运动的时间t2=2×10-2s,A从第一次进入盒子到第二次进入盒子的时间t=t1+t2=4×10-2s.(3)微粒运动一个周期盒子减少的速度为△v=a′(t1+t2)=2×(0.02+0.02)=0.08m/s
从小球第一次进入盒子到盒子停下,微粒球运动的周期数为n=
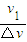 =
=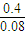 =5,故要保证小球始终不与盒子相碰,盒子上的小孔数至少为2n+1个,即11个.
=5,故要保证小球始终不与盒子相碰,盒子上的小孔数至少为2n+1个,即11个.答:(1)从微粒第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程为0.04m;
(2)微粒A从第一次进入盒子到第二次进入盒子所经历的时间为4×10-2s;
(3)盒子上至少要开11个小孔,才能保证微粒始终不与盒子接触.
点评:该题是较为复杂的往复运动,要求同学们能正确分析每个过程的受力情况,求出加速度、时间和位移,要求较高,难度适中.

练习册系列答案
相关题目
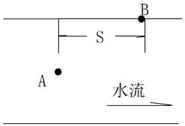 如图所示,航标灯修理工的一条小船位于200m宽的河正中A点处,从这里向下游100
如图所示,航标灯修理工的一条小船位于200m宽的河正中A点处,从这里向下游100 如图所示,a是地球赤道上一幢建筑物,b是在赤道平面内绕地球做匀速圆周运动的人造卫星,卫星运行轨道距离地面高度为h,某一时刻b刚好位于a的正上方(如图所示1,己知地球半径为R,地球表面重力加速度为g,地球自转周期为T′.求:
如图所示,a是地球赤道上一幢建筑物,b是在赤道平面内绕地球做匀速圆周运动的人造卫星,卫星运行轨道距离地面高度为h,某一时刻b刚好位于a的正上方(如图所示1,己知地球半径为R,地球表面重力加速度为g,地球自转周期为T′.求: (2009?奉贤区一模)如图所示,O为两个等量点电荷连线中点,P、M为连线中垂线上的位于连线同侧的任意两点,分别用φM、φP、EM、EP表示M、P两点的电势和场强的大小,则下列情况可能的是( )
(2009?奉贤区一模)如图所示,O为两个等量点电荷连线中点,P、M为连线中垂线上的位于连线同侧的任意两点,分别用φM、φP、EM、EP表示M、P两点的电势和场强的大小,则下列情况可能的是( )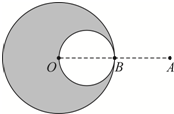 已知均匀带电球体在球的外部产生的电场与一个位于球心的、电荷量相等的点电荷产生的电场相同.如图所示,半径为R的球体上均匀分布着电荷量为Q的电荷,在过球心O的直线上有A、B两个点,O和B、B和A间的距离均为R.现以OB为直径在球内挖一球形空腔,若静电力常量为k,球的体积公式为V=
已知均匀带电球体在球的外部产生的电场与一个位于球心的、电荷量相等的点电荷产生的电场相同.如图所示,半径为R的球体上均匀分布着电荷量为Q的电荷,在过球心O的直线上有A、B两个点,O和B、B和A间的距离均为R.现以OB为直径在球内挖一球形空腔,若静电力常量为k,球的体积公式为V=