题目内容
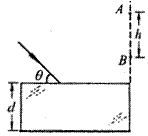
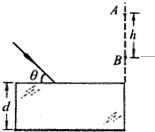 如图所示,真空中平行玻璃砖折射率为n=
如图所示,真空中平行玻璃砖折射率为n=| 2 |
分析:一束光斜射在表面镀反射膜的平行玻璃砖,则反射光线在竖直光屏上出现光点A,而折射光线经反射后再折射在竖直光屏上出现光点B,根据光学的几何关系可由AB两点间距确定CE间距,再由折射定律,得出折射角,最终算出玻璃砖的厚度.
解答:解:由题,单色光与界面成θ=45°,入射角θ1=45°,根据折射率公式 n=
,得sinθ2=
,θ2=30° 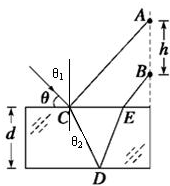
作出如图所示的光路,△CDE为等边三角形,四边形ABEC为梯形,CE=AB=h.玻璃的厚度d就是边长h的等边三角形的高.
故d=hcos30°=
h=1.732cm
答:玻璃砖的厚度d为1.732cm.
| sinθ1 |
| sinθ2 |
| 1 |
| 2 |

作出如图所示的光路,△CDE为等边三角形,四边形ABEC为梯形,CE=AB=h.玻璃的厚度d就是边长h的等边三角形的高.
故d=hcos30°=
| ||
| 2 |
答:玻璃砖的厚度d为1.732cm.
点评:本题根据光路可逆原理及光的反射定律可以证明AC与BE平行,从而确定CE的长度.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
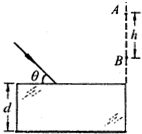 如图所示,真空中平行玻璃砖折射率为n=
如图所示,真空中平行玻璃砖折射率为n=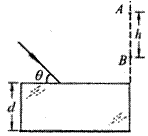 (6分)如图所示,真空中平行玻璃砖折射率为n =
(6分)如图所示,真空中平行玻璃砖折射率为n =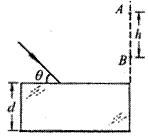
 如图所示,真空中平行玻璃砖折射率为n =
如图所示,真空中平行玻璃砖折射率为n =