题目内容
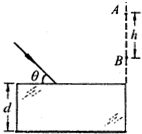 如图所示,真空中平行玻璃砖折射率为n=
如图所示,真空中平行玻璃砖折射率为n=| 2 |
(1)该单色光在玻璃砖中的传播速度;
(2)该单色光射入玻璃砖的折射角;
(3)玻璃砖的厚度d.
分析:(1)根据v=
求出光子爱玻璃砖中传播的速度.
(2)根据折射定律求出单色光射入玻璃砖的折射角.
(3)通过折射定律和几何关系求出玻璃砖的厚度.
| c |
| n |
(2)根据折射定律求出单色光射入玻璃砖的折射角.
(3)通过折射定律和几何关系求出玻璃砖的厚度.
解答: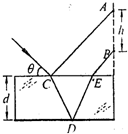 解:(1)由折射率公式n=
解:(1)由折射率公式n=
得:v=
=
×108m/s
(2)由折射率公式n=
,sinθ2=
=
,θ2=30°.
(3)作出如图所示的光路,△CDE为等边三角形,四边形ABEC为梯形,CE=AB=h.
玻璃的厚度d就是边长为h的等边三角形的高,故d=
h=1.7 cm.
答:(1)该单色光在玻璃砖中的传播速度为
×108m/s.
(2)该单色光射入玻璃砖的折射角为30°.
(3)玻璃砖的厚度d为1.7cm.
 解:(1)由折射率公式n=
解:(1)由折射率公式n=| c |
| v |
| c |
| n |
3
| ||
| 2 |
(2)由折射率公式n=
| sinθ1 |
| sinθ2 |
| sinθ1 |
| n |
| 1 |
| 2 |
(3)作出如图所示的光路,△CDE为等边三角形,四边形ABEC为梯形,CE=AB=h.
玻璃的厚度d就是边长为h的等边三角形的高,故d=
| ||
| 2 |
答:(1)该单色光在玻璃砖中的传播速度为
3
| ||
| 2 |
(2)该单色光射入玻璃砖的折射角为30°.
(3)玻璃砖的厚度d为1.7cm.
点评:本题考查了几何光学问题,难度不大,关键掌握折射率的两个公式v=
,n=
.
| c |
| n |
| sinθ1 |
| sinθ2 |

练习册系列答案
相关题目
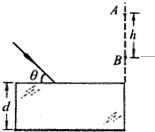 如图所示,真空中平行玻璃砖折射率为n=
如图所示,真空中平行玻璃砖折射率为n=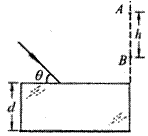 (6分)如图所示,真空中平行玻璃砖折射率为n =
(6分)如图所示,真空中平行玻璃砖折射率为n =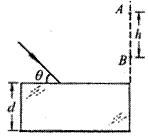
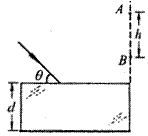 如图所示,真空中平行玻璃砖折射率为n =
如图所示,真空中平行玻璃砖折射率为n =