题目内容
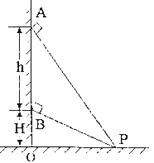
【题目】如图所示,在同一竖直线上有A、B两点,相距为h,B点离地高度为H。现从A、B两点分别向P点安放两个光滑的固定斜面AP和BP,并让两个小物块(可看成质点)从两斜面的A、B点同时由静止滑下,发现两小物块同时到达P点,则
A. OP间距离为![]()
B. OP间距离为![]()
C. 两小物块运动到P点速度相同
D. 两小物块的运动时间均为![]()
【答案】A
【解析】
物块沿光滑斜面下滑,根据牛顿第二定律可求出下滑的加速度,用底边OP的长度表示斜面的长度,运用运动公式求解时间关系式,由于时间相等,则可找到边长时间的关系;根据机械能守恒定律可知判断物块滑到P点的速度关系;对比自由落体运动的时间判断选项D.
AB.设斜面的倾角为θ,则物体下滑的加速度为a=gsinθ,设OP的距离为x,则![]() ,因两物体在斜面上下滑的时间相等,则sinθcosθ相等,由图可知:
,因两物体在斜面上下滑的时间相等,则sinθcosθ相等,由图可知:![]() ,解得
,解得![]() ,选项A正确,B错误;
,选项A正确,B错误;
C.根据机械能守恒定律可知:mgH1=![]() mv2可知,两物块开始下落的高度H1不同,则下落到底端的速度不同,选项C错误;
mv2可知,两物块开始下落的高度H1不同,则下落到底端的速度不同,选项C错误;
D.![]() 是物体从A点做自由落体运动到O点的时间,可知两小物块的运动时间均大于
是物体从A点做自由落体运动到O点的时间,可知两小物块的运动时间均大于![]() ,选项D错误;
,选项D错误;
故选A.

练习册系列答案
相关题目