题目内容
如图所示,有两个磁感应强度均为B、但方向相反的匀强磁场,OP是它们的分界面。有一束电量均为q、但质量不全相同的带电粒子,经过相同的电场加速后,从O处沿与OP和磁场都垂直的方向进入磁场,在这束粒子中有一些粒子的轨迹如图所示。已知OP=L,加速电场的电势差为U,重力不计,问。
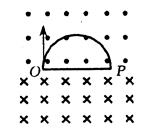
(1)按图示的轨迹到达P点的每个粒子的质量m为多大?
(2)在这束粒子中,质量为m的多少倍的粒子也可能到达P点?(设质量为m1)

(1)按图示的轨迹到达P点的每个粒子的质量m为多大?
(2)在这束粒子中,质量为m的多少倍的粒子也可能到达P点?(设质量为m1)
(1)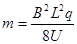 (2)
(2)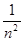
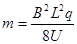 (2)
(2)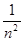
试题分析:粒子在电场中加速 qU=
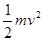
在磁场中轨道半径 r=

洛伦兹力提供向心力 qvB=
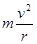
解得
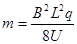
(2)设质量m1.粒子在电场中加速 qU=
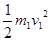
在磁场中轨道半径 L=n.2r1 (n=2.3.4…….)
洛伦兹力提供向心力 qv1B=
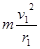
解得
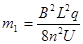
则质量为原质量的
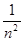 倍 (n=2.3.4……..)
倍 (n=2.3.4……..)点评:在垂直的磁场中做匀速圆周运动.圆周运动的可建立几何关系来列式求解.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 、
、 的狭长区域内,分布有磁感应强度为
的狭长区域内,分布有磁感应强度为 而方向垂直纸面向外的匀强磁场,磁场区域宽度为
而方向垂直纸面向外的匀强磁场,磁场区域宽度为 。一带正电的粒子,质量为
。一带正电的粒子,质量为 ,带电量为
,带电量为 ,以速率
,以速率 从左边界的O处斜向上射入磁场,粒子刚好从另一边界垂直射出,求:
从左边界的O处斜向上射入磁场,粒子刚好从另一边界垂直射出,求:



