题目内容
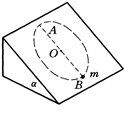
如图所示,长为2L的轻杆,两端各固定一小球,A球质量大于B球质量,杆的中点O有一水平光滑固定轴,杆可绕轴在竖直平面内转动。杆转至竖直时杆的角速度为ω,要使杆对转轴的作用力为零,则 球在上端,A、B两小球的质量之比为 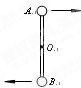
:A;(Lω2+g):(Lω2-g)
解析试题分析: 要使杆对转轴的作用力为零,杆对两球的作用力的大小相等,设杆对球的拉力均为F;两球均做圆周运动,合力充当向心力,
上面的球:F+m1g=m1ω2L ①;
下面的球:F-m2g=m2ω2L ②;
由①②两式解得,m1:m2=(Lω2+g):(Lω2-g);可知m1>m2,知A球在上端.
考点:向心力

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
如图(a)所示,小球与轻绳—端相连,绕另—端点O在竖直平面内作圆周运动,忽略一切阻力的影响,现测得绳子对小球的拉力随时间变化的图线如图(b)所示,则小球处于最高点位置的时刻是( ) 

| A.t1 | B.t2 | C.t3 | D.t4 |
如右图所示,长为L的轻杆A一端固定一个质量为m的小球B,另一端固定在水平转轴O上,轻杆A绕转轴O在竖直平面内匀速转动,角速度为ω.在轻杆A与水平方向夹角α从0°增加到90°的过程中,下列说法正确的是( )
| A.小球B受到轻杆A作用力的方向一定沿着轻杆A |
| B.小球B受到的合力的方向不一定沿着轻杆A |
| C.小球B受到轻杆A的作用力逐渐增大 |
| D.小球B受到轻杆A的作用力对小球B做正功 |
如图所示,MN是流速稳定的河流,河宽一定,小船在静水中的速度为v.现小船自A点渡河,第一次船头沿AB方向,到达对岸的D处;第二次船头沿AC方向,到达对岸E处,若AB与AC跟河岸垂线AD的夹角相等,两次航行的时间分别为tB、tC,则( )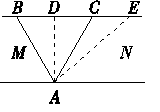
| A.tB>tC | B.tB<tC |
| C.tB=tC | D.无法比较tB与tC的大小 |
 、
、 、
、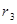 .若甲轮的角速度为
.若甲轮的角速度为 ,则丙轮的角速度为
,则丙轮的角速度为