题目内容
如图所示,一个带电小球用绝缘细线悬挂在匀强电场中,当悬线与竖直方向成60°角时,小球恰好在B点处于平衡状态,若线长为0.05m,小球质量为0.1kg,两板间的电场强度为
×106N/C,两板间距为
m,求:
(1)两金属板的电势差;
(2)小球的电荷量;
(3)如果将小球在悬点正下方的A点由静止释放,那么它到达B点时的速度为多大?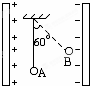
| 3 |
| ||
| 30 |
(1)两金属板的电势差;
(2)小球的电荷量;
(3)如果将小球在悬点正下方的A点由静止释放,那么它到达B点时的速度为多大?

(1)根据U=Ed得:
U=
×106×
V=1×105V
(2)小球在B点处于平衡状态,则有:
qE=mgtan60°
解得:q=1×10-6C
(3)从A到B的过程中运用动能定理得:
qELsin60°-mg(L-Lcos60°)=
mv2-0
解得:v=1m/s
答:(1)两金属板的电势差为1×105V;
(2)小球的电荷量为1×10-6C;
(3)如果将小球在悬点正下方的A点由静止释放,那么它到达B点时的速度为为1m/s.
U=
| 3 |
| ||
| 30 |
(2)小球在B点处于平衡状态,则有:
qE=mgtan60°
解得:q=1×10-6C
(3)从A到B的过程中运用动能定理得:
qELsin60°-mg(L-Lcos60°)=
| 1 |
| 2 |
解得:v=1m/s
答:(1)两金属板的电势差为1×105V;
(2)小球的电荷量为1×10-6C;
(3)如果将小球在悬点正下方的A点由静止释放,那么它到达B点时的速度为为1m/s.

练习册系列答案
相关题目
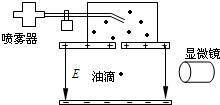
 电子所带的电量(基元电荷-e)最先是由密立根通过油滴实验测出的.密立根设计的实验装置如图所示:一个很小的带电油滴在电场内,调节电场,使作用在油滴上的电场力与油滴的重力平衡.如果在平衡时,油滴所在处的电场强度为E,油滴的半径为r,油滴的密度为ρ(油滴可看作球形),重力加速度取g.则油滴所在处的电场方向
电子所带的电量(基元电荷-e)最先是由密立根通过油滴实验测出的.密立根设计的实验装置如图所示:一个很小的带电油滴在电场内,调节电场,使作用在油滴上的电场力与油滴的重力平衡.如果在平衡时,油滴所在处的电场强度为E,油滴的半径为r,油滴的密度为ρ(油滴可看作球形),重力加速度取g.则油滴所在处的电场方向 如图所示,一个带电粒子从粒子源飘入(初速度很小,可忽略不计)电压为U1的加速电场,经加速后从小孔S沿平行金属板A、B的中心线射入,A、B板长为L,相距为d,电压为U2,则带电粒子能从A、B板间飞出应该满足的条件是(不计粒子重力)( )
如图所示,一个带电粒子从粒子源飘入(初速度很小,可忽略不计)电压为U1的加速电场,经加速后从小孔S沿平行金属板A、B的中心线射入,A、B板长为L,相距为d,电压为U2,则带电粒子能从A、B板间飞出应该满足的条件是(不计粒子重力)( )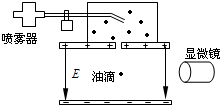 电子所带的电荷量(元电荷)最先是由密立根通过油滴实验测出的.密立根设计的实验装置如图所示.一个很小的带电油滴在电场内,调节场强E,使作用在油滴上的电场力与油滴的重力平衡.如果油滴的质量是1.57×10-14kg,在平衡时电场强度E=1.92×105 N/C.由此可判定:这个带电油滴上带
电子所带的电荷量(元电荷)最先是由密立根通过油滴实验测出的.密立根设计的实验装置如图所示.一个很小的带电油滴在电场内,调节场强E,使作用在油滴上的电场力与油滴的重力平衡.如果油滴的质量是1.57×10-14kg,在平衡时电场强度E=1.92×105 N/C.由此可判定:这个带电油滴上带