题目内容
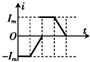
9.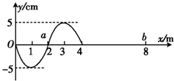 一列简谐横波沿 x 轴正方向传播,t=0时刻刚好传播到x=4m的位置,波形如图所示,介质中的质点a、b平衡位置坐标分别为xa=2m和xb=8m,已知a再经过0.3s第一次到达波峰位置,则这列波的波速为10m/s;质点b刚开始振动时的运动方向为沿y轴正方向;质点b第一次到达波峰的时刻为0.5s.
一列简谐横波沿 x 轴正方向传播,t=0时刻刚好传播到x=4m的位置,波形如图所示,介质中的质点a、b平衡位置坐标分别为xa=2m和xb=8m,已知a再经过0.3s第一次到达波峰位置,则这列波的波速为10m/s;质点b刚开始振动时的运动方向为沿y轴正方向;质点b第一次到达波峰的时刻为0.5s.
分析 根据质点带动法知,a点经过$\frac{3}{4}$第一次到波峰,可以求周期,从而求波速.沿波的传播方向,个质点的振动方向是相同的;利用b点到波峰的距离除以波速得到第一次到达波峰的时间.
解答 解:(1)简谐横波沿x轴正方向传播,a点开始向下运动,经$\frac{3}{4}$T 到达波峰,则t1=$\frac{3}{4}$T
解得 T=0.4s
波速 v=$\frac{λ}{T}=\frac{4}{0.4}=10$ m/s
(2)由图可知,x=4m处的质点起振的方向向上,所以质点b刚开始振动时的运动方向沿y轴向上.
(3)质点b第一次到达波峰时,波传播的位移为 x=5m
所用时间 t2=$\frac{x}{v}=\frac{5}{10}$=0.5s
故答案为:10,沿y轴正方向,0.5
点评 本题考查了波的传播过程中质点振动方向的判断,周期、波速的求法.要熟练运用质点的带动法判断质点的振动方向.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.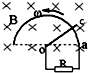 如图所示,在磁感强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架,OC为一能绕O在框架上滑动的导体棒,OC之间连一个电阻R,导体框架与导体棒的电阻均不计,若要使OC能以角速度ω匀速转动,则外力做功的功率是( )
如图所示,在磁感强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架,OC为一能绕O在框架上滑动的导体棒,OC之间连一个电阻R,导体框架与导体棒的电阻均不计,若要使OC能以角速度ω匀速转动,则外力做功的功率是( )
 如图所示,在磁感强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架,OC为一能绕O在框架上滑动的导体棒,OC之间连一个电阻R,导体框架与导体棒的电阻均不计,若要使OC能以角速度ω匀速转动,则外力做功的功率是( )
如图所示,在磁感强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架,OC为一能绕O在框架上滑动的导体棒,OC之间连一个电阻R,导体框架与导体棒的电阻均不计,若要使OC能以角速度ω匀速转动,则外力做功的功率是( )| A. | $\frac{{B}^{2}{r}^{2}{ω}^{4}}{4R}$ | B. | $\frac{{B}^{2}{r}^{4}{ω}^{2}}{4R}$ | C. | $\frac{{B}^{2}{r}^{4}{ω}^{2}}{2R}$ | D. | $\frac{{B}^{2}{r}^{4}{ω}^{2}}{9R}$ |
20.模拟我国志愿者王跃曾与俄罗斯志愿者一起进行“火星500”的实验活动.假设王跃登陆火星后,测得火星的半径是地球半径的$\frac{1}{2}$,质量是地球质量的$\frac{1}{9}$.已知地球表面的重力加速度是g,地球的半径为R,王跃在地面上能向上竖直跳起的最大高度是h,忽略天体自转的影响,下列说法正确的是( )
| A. | 火星的密度为$\frac{2g}{3πGR}$ | |
| B. | 火星表面的重力加速度是$\frac{2g}{9}$ | |
| C. | 火星的第一宇宙速度与地球的第一宇宙速度之比为$\frac{2}{3}$ | |
| D. | 王跃在火星表面上能向上竖直跳起的最大高度也是h |
18.我们经常在电视中看到男、女花样滑冰运动员手拉手在冰面上旋转并表演各种优美的动作.现有甲、乙两名花样滑冰运动员,M甲=80kg,M乙=40kg,他们面对面拉着弹簧测力计各自以他们连线上某一点为圆心做匀速圆周运动,若两人相距0.9m,弹簧测力计的示数为600N,则( )
| A. | 两人的线速度相同,为0.4 m/s | |
| B. | 两人的角速度相同,为5.0 rad/s | |
| C. | 两人的运动半径相同,都是0.45 m | |
| D. | 两人的运动半径不同,甲的半径是0.3m、乙的半径是0.6 m |
19.两个物体做匀速圆周运动,在相同的时间内,它们通过的路程之比为4:3,运动方向改变的角度之比为3:2,它们的向心加速度之比为( )
| A. | 2:1 | B. | 1:2 | C. | 8:9 | D. | 9:8 |

 如图所示,有一个边界为正三角形的匀强磁场区域,边长为a,磁感应强度方向垂直纸面向里,一个矩形导体框的长为a、宽为.若导体框平行于纸面沿着磁场区域的轴线匀速穿越磁场区域,取导体框中感应电流的逆时针方向为正方向,以导体框刚进入磁场时为t=0时刻.则在穿过磁场的过程中,导体框中的感应电流随时间变化的图象是图中的( )
如图所示,有一个边界为正三角形的匀强磁场区域,边长为a,磁感应强度方向垂直纸面向里,一个矩形导体框的长为a、宽为.若导体框平行于纸面沿着磁场区域的轴线匀速穿越磁场区域,取导体框中感应电流的逆时针方向为正方向,以导体框刚进入磁场时为t=0时刻.则在穿过磁场的过程中,导体框中的感应电流随时间变化的图象是图中的( )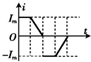

 如图所示,AB是一个接地的很大的薄金属板,其右侧P点有一带电量为Q的正点电荷,N为金属板右侧表面上的一点,P到金属板的垂直距离PN=d,M为PN连线的中点.关于M,N两点的场强和电势,有如下说法:
如图所示,AB是一个接地的很大的薄金属板,其右侧P点有一带电量为Q的正点电荷,N为金属板右侧表面上的一点,P到金属板的垂直距离PN=d,M为PN连线的中点.关于M,N两点的场强和电势,有如下说法: