题目内容
1.用单摆测定当地的重力加速度:在“用单摆测定重力加速度”的实验中,测出单摆摆角小于5°时,完成n次全振动的时间为t,用毫米刻度尺测得摆线长为L,用螺旋测微器测得摆球直径为d.
(1)用上述物理量的符号写出测重力加速度的一般表达式:g=$\frac{4{n}^{2}{π}^{2}(L+\frac{d}{2})}{{t}^{2}}$.
(2)要在摆球通过平衡位置时开始计时
(3)实验中,有个同学发现他测得的当地重力加速度总是偏大,其原因可能是D
A.实验室处在高山上,距离水平面太高
B.单摆所用的摆球太重了
C.测出n次全振动的时间t,误作为(n-1)次全振动的时间进行计算
D.以摆线长与摆球直径之和作为摆长来计算.
分析 由秒表测出单摆完成n次全振动所用时间为t,可得单摆周期T,由单摆周期公式T=2π$\sqrt{\frac{L}{g}}$可得重力加速度g,然后根据公式说明.数次数时应从平衡位置开始计时.
解答 解:(1)根据单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$推导出重力加速度的表达式:g=$\frac{4{π}^{2}L}{{T}^{2}}$.
(2)数次数时应从平衡位置开始计时,此位置速度大,变化快,容易数次数,故为:平衡
(3)若测得的当地重力加速度总是偏大,有两种可能:L的测量值偏大,或T的测量值偏小.
A、实验室处在高山上,距离水平面太高,因为越往高处,根据万有引力定律知物体与地球之间的吸引力越小,则测得的当地的加速度结果偏小,故A错误;
B、根据公式,单摆的周期与摆球的质量无关.故B错误;
C、测出次n全振动的时间t,误作为(n-1)次全振动的时间进行计算,则:T测=$\frac{t}{n-1}$>$\frac{t}{n}$=T真,周期的测量值偏大,测得的g会偏小.故C错误;
D、以摆线长与摆球直径之和作为摆长来计算,L测=l+d>l+$\frac{d}{2}$=L真即摆长的测量值偏大,测得的结果偏大.故D正确.
故选:D.
故答案为:(1)$\frac{4{n}^{2}{π}^{2}(L+\frac{d}{2})}{{t}^{2}}$,(2)平衡,(3)D
点评 熟练应用单摆周期公式T=2π$\sqrt{\frac{L}{g}}$导出重力加速度的表达式:g=$\frac{4{π}^{2}L}{{T}^{2}}$.然后根据公式说明,即可正确解题.属于中档题目

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
11.许多物理学家在物理学的发展过程中做出了重要贡献,在物理史实和物理方法方面,下列表述正确的是( )
| A. | 牛顿通过实验研究了自由落体运动的规律 | |
| B. | 法拉第概括总结了法拉第电磁感应定律和判断感应电流方向的规律 | |
| C. | 比值定义法包括:电场强度E=$\frac{F}{q}$;电容C=$\frac{Q}{U}$;电阻R=$\frac{U}{I}$;加速度a=$\frac{F}{m}$ | |
| D. | 在牛顿发现万有引力定律的过程中,胡克曾给予了很大的帮助 |
16. 如图是街头变压器通过降压给用户供电的示意图.变压器输入电压是市电网的电压,不会有很大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器触头P向下移时( )
如图是街头变压器通过降压给用户供电的示意图.变压器输入电压是市电网的电压,不会有很大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器触头P向下移时( )
 如图是街头变压器通过降压给用户供电的示意图.变压器输入电压是市电网的电压,不会有很大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器触头P向下移时( )
如图是街头变压器通过降压给用户供电的示意图.变压器输入电压是市电网的电压,不会有很大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器触头P向下移时( )| A. | 相当于在减少用电器的数目 | |
| B. | A1表的示数随A2表的示数的增大而增大 | |
| C. | V1表的示数随V2表的示数的增大而增大 | |
| D. | 变压器的输入功率在增大 |
10.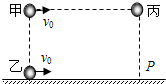 甲、乙、丙三个小球(均视为质点)分别位于如图所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,与乙在同一水平面上的P点在丙的正下方,在同一时刻甲、乙、丙开始运动,甲以水平速度v0向右平抛,乙以水平速度v0沿水平面向右做匀速直线运动,丙做自由落体运动,不计空气阻力,则( )
甲、乙、丙三个小球(均视为质点)分别位于如图所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,与乙在同一水平面上的P点在丙的正下方,在同一时刻甲、乙、丙开始运动,甲以水平速度v0向右平抛,乙以水平速度v0沿水平面向右做匀速直线运动,丙做自由落体运动,不计空气阻力,则( )
 甲、乙、丙三个小球(均视为质点)分别位于如图所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,与乙在同一水平面上的P点在丙的正下方,在同一时刻甲、乙、丙开始运动,甲以水平速度v0向右平抛,乙以水平速度v0沿水平面向右做匀速直线运动,丙做自由落体运动,不计空气阻力,则( )
甲、乙、丙三个小球(均视为质点)分别位于如图所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,与乙在同一水平面上的P点在丙的正下方,在同一时刻甲、乙、丙开始运动,甲以水平速度v0向右平抛,乙以水平速度v0沿水平面向右做匀速直线运动,丙做自由落体运动,不计空气阻力,则( )| A. | 若只有甲、乙两球在水平面上相遇,此时丙球还未着地落到P点 | |
| B. | 无论初速度v0大小如何,甲、乙、丙三球一定不会同时在P点相遇 | |
| C. | 甲、乙、丙三球可能同时相遇在P点 | |
| D. | 若甲、丙两球在空中相遇,此时乙球一定在P点 |
11.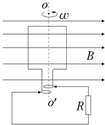 如图所示,有一矩形线圈面积为S,匝数为N,总电阻为r,外电阻为R,接触电阻不计.线圈绕垂直于磁感线的轴OO′以角速度ω匀速转动,匀强磁场的磁感应强度为B.则( )
如图所示,有一矩形线圈面积为S,匝数为N,总电阻为r,外电阻为R,接触电阻不计.线圈绕垂直于磁感线的轴OO′以角速度ω匀速转动,匀强磁场的磁感应强度为B.则( )
 如图所示,有一矩形线圈面积为S,匝数为N,总电阻为r,外电阻为R,接触电阻不计.线圈绕垂直于磁感线的轴OO′以角速度ω匀速转动,匀强磁场的磁感应强度为B.则( )
如图所示,有一矩形线圈面积为S,匝数为N,总电阻为r,外电阻为R,接触电阻不计.线圈绕垂直于磁感线的轴OO′以角速度ω匀速转动,匀强磁场的磁感应强度为B.则( )| A. | 当线圈平面与磁感线平行时,线圈中电流强度最大 | |
| B. | 电流有效值I=$\frac{\sqrt{2}NBSω}{R+r}$ | |
| C. | 外力做功的平均功率P=$\frac{(NBSω)^{2}}{R+r}$ | |
| D. | 当线圈平面与磁感线平行时开始转动90°过程中,通过电阻的电量为$\frac{NBS}{R+r}$ |
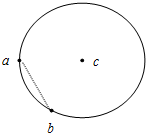 如图所示,半径为R的圆形区域,c为圆心,在圆上a点有一粒子源以相同的速率向圆面内各个方向发射多个质量为m、电荷量为+q 的带电粒子.当圆形区域存在垂直于圆面、磁感应强度大小为B的匀强磁场时,沿ac方向射入的粒子从b 点离开场区,此过程粒子速度方向偏转了$\frac{2π}{3}$.若只将圆形区域内的磁场换成平行于圆面的匀强电场,粒子从电场圆边界的不同位置射出时有不同的动能,其最大动能是初动能的4倍,经过b点的粒子在 b点的动能是初动能的3倍.不计粒子重力及粒子间的相互作用.求:
如图所示,半径为R的圆形区域,c为圆心,在圆上a点有一粒子源以相同的速率向圆面内各个方向发射多个质量为m、电荷量为+q 的带电粒子.当圆形区域存在垂直于圆面、磁感应强度大小为B的匀强磁场时,沿ac方向射入的粒子从b 点离开场区,此过程粒子速度方向偏转了$\frac{2π}{3}$.若只将圆形区域内的磁场换成平行于圆面的匀强电场,粒子从电场圆边界的不同位置射出时有不同的动能,其最大动能是初动能的4倍,经过b点的粒子在 b点的动能是初动能的3倍.不计粒子重力及粒子间的相互作用.求: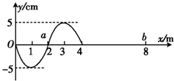 一列简谐横波沿 x 轴正方向传播,t=0时刻刚好传播到x=4m的位置,波形如图所示,介质中的质点a、b平衡位置坐标分别为xa=2m和xb=8m,已知a再经过0.3s第一次到达波峰位置,则这列波的波速为10m/s;质点b刚开始振动时的运动方向为沿y轴正方向;质点b第一次到达波峰的时刻为0.5s.
一列简谐横波沿 x 轴正方向传播,t=0时刻刚好传播到x=4m的位置,波形如图所示,介质中的质点a、b平衡位置坐标分别为xa=2m和xb=8m,已知a再经过0.3s第一次到达波峰位置,则这列波的波速为10m/s;质点b刚开始振动时的运动方向为沿y轴正方向;质点b第一次到达波峰的时刻为0.5s.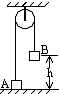 如图,跨过光滑的定滑轮的细线两端各系住物体A和B,已知两物体的质量分别是mA=0.1kg,mB=0.3kg,开始时将A用手揿住在地面上,放手后发现A能升起的最大高度为0.9m,问B物体原来离地面的高度h等于多少?
如图,跨过光滑的定滑轮的细线两端各系住物体A和B,已知两物体的质量分别是mA=0.1kg,mB=0.3kg,开始时将A用手揿住在地面上,放手后发现A能升起的最大高度为0.9m,问B物体原来离地面的高度h等于多少?