Question

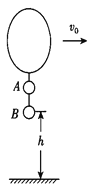
【题目】如图所示，气球下面吊着A、B两个小球，B球离水平地面高为h，整个系统以大小为的速度沿水平方向匀速前进，气球和小球A的总质量为M，小球B的质量为m，重力加速度大小为g，不计小球A、B的大小，不计空气阻力，气球所受浮力始终不变，某时刻A、B间的细线断开，求：

(1)A、B间细线断开后，小球B运动的水平位移大小；

(2)小球B落地时，空气浮力对气球做的功及气球离小球B的距离。

Answer 1

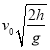【答案】(1)；(2)，

【解析】

(1)细线断开后，小球B做平拋运动，设小球B在空中运动时间为t，则

解得

这段时间内小球B的水平位移

(2)细线断开后，气球做类平拋运动，设气球受到的浮力为F，细线断前，根据力的平衡

细线断后，对气球根椐牛顿第二定律

解得

则气球在t时间内上升的高度

空气浮力对气球做的功

气球离地面的高度

由于小球B和气球在水平方向速度相同，因此小球B在空中运动过程中，始终在气球的正下方，因此小球B落地时，气球离小球B的距离为。