题目内容
5. 空间存在范围足够大的水平方向匀强电场,长为L的绝缘细线一断固定于O点,另一端系一带电量为正q质量为m小球,已知电场强度E=$\frac{3mg}{4q}$.OA处于水平方向,OC在竖直方向.小球从A点由静止释放,当小球运动到O点正下方B时细线恰好断裂(取sin37°=0.6,cos37°=0.8).求:
空间存在范围足够大的水平方向匀强电场,长为L的绝缘细线一断固定于O点,另一端系一带电量为正q质量为m小球,已知电场强度E=$\frac{3mg}{4q}$.OA处于水平方向,OC在竖直方向.小球从A点由静止释放,当小球运动到O点正下方B时细线恰好断裂(取sin37°=0.6,cos37°=0.8).求:(1)小球从A点运动到B点过程中的最大速率;
(2)当小球再次运动到OC线上的D点时,小球速度的大小和方向;
(3)BD的高度.
分析 (1)对小球从A到B过程应用动能定理可以求出小球的最大速度.
(2)由动能定理求出到达B点的速度,绳子断裂后小球做平抛运动,应用平抛运动规律可以求出小球的速度.
(3)绳子断裂后小球做平抛运动,在竖直方向做自由落体运动,由自由落体运动的位移公式可以求出高度.
解答 解:(1)因为电场力与重力的合力方向与竖直方向成37°,所以当小球运动到细线与竖直方向成37°时速率最大.由动能定理得:
mgLcos37°-qE(L-Lsin37°)=$\frac{1}{2}$mvm2-0,
解得:vm=$\sqrt{gL}$;
(2)S设小球运动到B点时速度大小为vB,由动能定理得:mgL-qEL=$\frac{1}{2}$mvB2-0,
解得:vB=$\sqrt{\frac{gL}{2}}$,
细线断裂后,小球水平方向作匀减速运动,竖直方向作自由落体运动.
水平方向加速度:a=$\frac{qE}{m}$=$\frac{3}{4}$g,
小球再次运动到OC线上的D点所需时间:t=$\frac{2{v}_{B}}{a}$=$\frac{4\sqrt{2gL}}{3g}$,
小球到D点时竖直方向的速度:vy=gt=$\frac{4\sqrt{2gL}}{3}$,
水平方向的速度:vx=$\sqrt{\frac{gL}{2}}$,
小球的速度:v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=$\sqrt{\frac{73gL}{18}}$,
设小球的速度方向与竖直方向成θ角,则:tanθ=$\frac{{v}_{x}}{{v}_{y}}$=$\frac{3}{8}$;
(3)BD的高度:h=$\frac{1}{2}$gt2=$\frac{16}{9}$L;
答:(1)小球从A点运动到B点过程中的最大速率为$\sqrt{gL}$;
(2)当小球再次运动到OC线上的D点时,小球速度的大小为$\sqrt{\frac{73gL}{18}}$,方向:与竖直方向夹角为:arctan$\frac{3}{8}$;
(3)BD的高度为$\frac{16}{9}$L.
点评 本题是一道力学综合题,物体运动过程复杂,难度较大,分析清楚物体运动过程是正确解题的关键,分析清楚运动过程后,应用动能定理、平抛运动规律可以解题.

 阅读快车系列答案
阅读快车系列答案| A. | 法拉第发现了电磁感应现象,使人类迈进了使用电的时代 | |
| B. | 20世纪初,爱因斯坦建立了狭义相对论,得出了一些不同于经典力学的观念和结论 | |
| C. | 欧姆用实验研究了电流的热效应,总结出欧姆定律 | |
| D. | 19世纪中叶,焦耳和楞次先后各自独立发现了电流通过导体时产生热效应的规律,称为焦耳-楞次定律 |
| A. | 布朗运动是液体分子的无规则运动 | |
| B. | 布朗运动是指悬浮在液体中的固体分子的无规则运动 | |
| C. | 沸腾的开水中撒一些胡椒粉,可以研究布朗运动 | |
| D. | 观察布朗运动会看到,悬浮的颗粒越小,温度越高,布朗运动越剧烈 |
| A. | 在空中任何时刻总是排成抛物线,它们的落地点是等间距的 | |
| B. | 在空中任何时刻总是排成抛物线,它们的落地点是不等间距的 | |
| C. | 在空中任何时刻总在飞机正下方,排成竖直的直线,它们的落地点是等间距的 | |
| D. | 在空中任何时刻总在飞机的正下方,排成竖直的直线,它们的等间距的 |
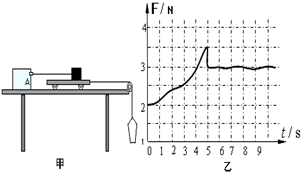 在探究摩擦力变化规律的实验中,特设计了如甲图所示的演示装置,力传感器A与计算机连接,可获得力随时间变化的规律,将力传感器固定在光滑水平桌面上,测力端通过细绳与一滑块相连(调节传感器高度可使细绳水平),滑块放在较长的小车上,小车一端连接一根轻绳并跨过光滑的轻定滑轮系一只空沙桶(调节滑轮可使桌面上部细绳水平),整个装置处于静止状态.实验开始时打开传感器同时缓慢向沙桶里倒入沙子,小车一旦运动起来,立即停止倒沙子,若力传感器采集的图象如乙图所示,则结合该图象,下列说法中正确的是( )
在探究摩擦力变化规律的实验中,特设计了如甲图所示的演示装置,力传感器A与计算机连接,可获得力随时间变化的规律,将力传感器固定在光滑水平桌面上,测力端通过细绳与一滑块相连(调节传感器高度可使细绳水平),滑块放在较长的小车上,小车一端连接一根轻绳并跨过光滑的轻定滑轮系一只空沙桶(调节滑轮可使桌面上部细绳水平),整个装置处于静止状态.实验开始时打开传感器同时缓慢向沙桶里倒入沙子,小车一旦运动起来,立即停止倒沙子,若力传感器采集的图象如乙图所示,则结合该图象,下列说法中正确的是( )| A. | 可求出空沙桶的重力 | |
| B. | 可求出滑块与小车之间的滑动摩擦力的大小 | |
| C. | 可求出滑块与小车之间的最大静摩擦力的大小 | |
| D. | 可判断第5秒后小车做匀速直线运动(滑块仍在车上) |
| A. | 用光导纤维传播信号 | |
| B. | 用透明的标准样板和单色光检查平面的平整度 | |
| C. | 对着日光灯从两铅笔的狭缝中看到的彩色条纹 | |
| D. | 太阳光斜射在铁栅栏上,地面出现明暗相间的条纹 |
 在“用油膜法估测分子的大小”的实验中,所用油酸酒精溶液的浓度为每104 mL溶液中有纯油酸6mL,用注射器测得1mL上述溶液为75滴.把1滴该溶液滴入盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,用彩笔在玻璃板上描出油膜的轮廊,再把玻璃板放在坐标纸上,其形状和尺寸如图所示,坐标中正方形方格的边长为1cm.则
在“用油膜法估测分子的大小”的实验中,所用油酸酒精溶液的浓度为每104 mL溶液中有纯油酸6mL,用注射器测得1mL上述溶液为75滴.把1滴该溶液滴入盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,用彩笔在玻璃板上描出油膜的轮廊,再把玻璃板放在坐标纸上,其形状和尺寸如图所示,坐标中正方形方格的边长为1cm.则