题目内容
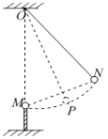
【题目】如图所示,在竖直向下磁感应强度为B的匀强磁场中,有两根间距为L竖直放置的平行粗糙导轨CD、EF,质量为m的金属棒MN与导轨始终垂直且接触良好,它们之间的动摩擦因数为μ。从t=0时刻起,给金属棒通以图示方向的电流且电流强度与时间成正比,即I=kt,(k为常量),则金属棒由静止下滑过程中加速度和速度的变化情况是 ____________金属棒下落过程中动能最大的时刻t=_____ 。

【答案】金属棒由静止下滑过程中加速度是先减后增最后为零,速度是先增后减最后为零 ![]()
【解析】
[1]当从t=0时刻起,金属棒通以电流I=kt,则由左手定则可知,安培力方向垂直纸面向里,使其紧压导轨
![]()
根据牛顿第二定律
![]()
所以加速度在减小,由于速度与加速度方向相同,则做加速度减小的加速运动。
当滑动摩擦力等于重力时,加速度为零,则速度达到最大,其动能也最大。
当安培力继续增大时,导致加速度方向竖直向上,根据牛顿第二定律
![]()
则出现加速度与速度方向相反,因此做加速度增大的减速运动。
当速度减到零后,由于重力小于最大静摩擦力,所以静止。
故金属棒由静止下滑过程中加速度是先减后增最后为零,速度是先增后减最后为零。
[2] 当滑动摩擦力等于重力时,加速度为零,则速度达到最大,其动能也最大。有
![]()
解得
![]()

练习册系列答案
相关题目