题目内容

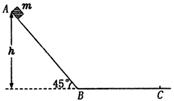
 (14分) 如图所示，AB为斜轨道，与水平方向成45°角，BC为水平轨道，两轨道在B处通过一段小圆弧相连接，一质量为m的小物块，自轨道AB的A处从静止开始沿轨道下滑，最后停在轨道上的C点，已知A点高h，物块与轨道间的滑动摩擦系数为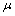，求：

（1）在整个滑动过程中摩擦力所做的功．

（2）物块沿轨道AB段滑动时间t1与沿轨道BC段滑动时间t2之比值．

（3）使物块匀速地、缓慢地沿原路回到A点所需做的功．
 
 

 

 

 

 

 

 

 

【答案】

 （1）设整个过程摩擦力做的功是W，由动能定理得：mgh－W=0    ①  

W=mgh                                       3分

（2）设物块沿轨道AB滑动的加速度为a1，

由牛顿第二定律有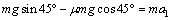  ②                  2分

设物块到达B点时的速度为VB，则有VB=a1t1   ③                      2分

设物块沿轨道BC滑动的加速度为a2，由牛顿第二定律有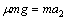    ④                 2分

物块从B点开始作匀减速运动，到达C点时，速度为零，故有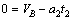    ⑤            2分

由②③④⑤式可得：    ⑥                         3分

（3）使物块匀速地、缓慢地沿原路回到A点所需做的功应该是克服重力和阻力所做功之和，即是

W1=mgh＋W=2mgh                         3分

 

练习册系列答案
相关题目

（本题14分）如图所示，AB为水平轨道，A、B间距离s=1m，BCD是半径为R=0.2m的竖直半圆形轨道，B为两轨道的连接点，D为轨道的最高点，整个轨道处于竖直向下的匀强电场中，场强大小为E=。一带正电的小物块质量为m=0.5kg，它与水平轨道间的动摩擦因数均为μ=0.1。小物块在F=10N的水平恒力作用下从A点由静止开始运动，到达B点时撤去力F，小物块刚好能到达D点，试求：(g=10m/s2)

（1）撤去F时小物块的速度大小；

（2）在半圆形轨道上小物块克服摩擦力做的功。

 

 

 

 

 

 

(14分）如图所示，质量M=0.2kg的长板静止在水平地面上，与地面间动摩擦因数μ1＝0.1，另一质量m=0.1kg的带正电小滑块以v0=8m/s初速滑上长木板，滑块与长木板间动摩擦因数μ2＝0.5，小滑块带电量为q＝2×10－3C，整个运动过程始终处于水平向右的匀强电场中，电场强度E＝1×102N/C，（m/s2）求：

（1）刚开始时小滑块和长板的加速度大小各为多少.

（2）小滑块最后停在距木板左端多远的位置.

（3）整个运动过程中产生的热量.

 

(14分）如图所示，高为0.3m的水平通道内，有一个与之等高的质量为M＝1.2kg表面光滑的立方体，长为L＝0.2m的轻杆下端用铰链连接于O点，O点固定在水平地面上竖直挡板的底部（挡板的宽度可忽略），轻杆的上端连着质量为m＝0.3kg的小球，小球靠在立方体左侧。取g＝10m/s2，sin37°＝0.6，cos37°＝0.8。

（1）为了使轻杆与水平地面夹角＝37°时立方体平衡且不动，作用在立方体上的水平推力F1应为多大？

（2）若立方体在F2＝4.5N的水平推力作用下从上述位置由静止开始向左运动，则刚要与挡板相碰时其速度多大？

（3）立方体碰到挡板后即停止运动，而轻杆带着小球向左倒下碰地后反弹恰好能回到竖直位置，若小球与地面接触的时间为t＝0.05s，则小球对地面的平均冲击力为多大？

（4）当杆回到竖直位置时撤去F2，杆将靠在立方体左侧渐渐向右倒下，最终立方体在通道内的运动速度多大？

 

（本小题14分）如图所示为车站使用的水平传送带的模型，它的水平传送带的长度为L=8 m，传送带的皮带轮的半径均为R=0．2 m，传送带的上部距地面的高度为h=0．45 m，现有一个旅行包（视为质点）以v0=10 m/s的初速度水平地滑上水平传送带。已知旅行包与皮带之间的动摩擦因数为 µ=0．6． （g取10 m/s2．）试讨论下列问题：

（1）若传送带静止，旅行包滑到B端时，人若没有及时取下，旅行包将从B端滑落。则包的落地点距B端的水平距离为多少?

（2）设皮带轮顺时针匀速转动，并设水平传送带长度仍为8 m，旅行包滑上传送带的初速度恒为10 m/s。当皮带轮的角速度ω值在什么范围内，旅行包落地点距B端的水平距离始终为（1）中所求的水平距离?若皮带轮的角速度ω1=40 rad/s，旅行包落地点距B端的水平距离又是多少?

（3）设皮带轮以不同的角速度顺时针匀速转动，在图所示的坐标系中画出旅行包落地点距B端的水平距离s随皮带轮的角速度ω变化的图象．

 

（本题14分）如图所示，AB为水平轨道，A、B间距离s=1m，BCD是半径为R=0.2m的竖直半圆形轨道，B为两轨道的连接点，D为轨道的最高点，整个轨道处于竖直向下的匀强电场中，场强大小为E=。一带正电的小物块质量为m=0.5kg，它与水平轨道间的动摩擦因数均为μ=0.1。小物块在F=10N的水平恒力作用下从A点由静止开始运动，到达B点时撤去力F，小物块刚好能到达D点，试求：(g=10m/s2)

（1）撤去F时小物块的速度大小；

（2）在半圆形轨道上小物块克服摩擦力做的功。

 

 

 

 

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网