Question

（本小题14分）如图所示为车站使用的水平传送带的模型，它的水平传送带的长度为L=8 m，传送带的皮带轮的半径均为R=0．2 m，传送带的上部距地面的高度为h=0．45 m，现有一个旅行包（视为质点）以v₀=10 m/s的初速度水平地滑上水平传送带。已知旅行包与皮带之间的动摩擦因数为 µ=0．6． （g取10 m/s²．）试讨论下列问题：

（1）若传送带静止，旅行包滑到B端时，人若没有及时取下，旅行包将从B端滑落。则包的落地点距B端的水平距离为多少?

（2）设皮带轮顺时针匀速转动，并设水平传送带长度仍为8 m，旅行包滑上传送带的初速度恒为10 m/s。当皮带轮的角速度ω值在什么范围内，旅行包落地点距B端的水平距离始终为（1）中所求的水平距离?若皮带轮的角速度ω₁=40 rad/s，旅行包落地点距B端的水平距离又是多少?

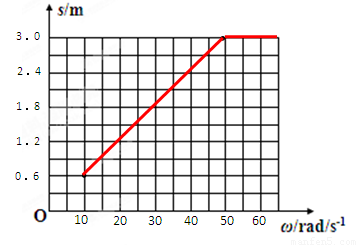
（3）设皮带轮以不同的角速度顺时针匀速转动，在图所示的坐标系中画出旅行包落地点距B端的水平距离s随皮带轮的角速度ω变化的图象．

 

Answer 1

【答案】

（1）x=0.6m

（2）；

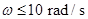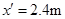
（3）略

【解析】本题考查力与运动的关系，先对旅行包进行受力分析，摩擦力提供加速度，旅行包到达B段的速度与圆周的临界速度进行对比可知旅行包做平抛运动，根据竖直高度求得运动时间再由水平方向的匀速运动求得水平位移，当ω₁=40rad/s时，求得线速度大小，与旅行包的速度比较可由运动学公式求得位移大小，以后旅行包做匀速直线运动

旅行包做匀减速运动a=μg=6m/s²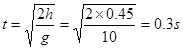（1分）（1分）

（1）旅行包到达B端速度为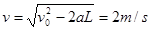，（1分）

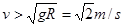 ，所以包作平抛运动（1分）

包的落地点距B端的水平距离为：s=vt=2×0.3m="0.6m" （1分）

（2）当ω₁=40rad/s时，皮带速度为v₁=ω₁R="8m/s" (1分)

设当旅行包的速度也为v₁=8m/s时，可得在皮带上运动了位移，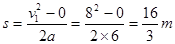 

以后旅行包做匀速直线运动，所以旅行包到达B端的速度也为v₁="8m/s" 作平抛运动（2分） ，

包的落地点距B端的水平距离为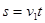="2.4m" （1分）

（3）如图所示 （3分）