题目内容
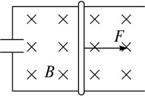
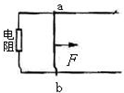如图所示，位于同一水平面内的、两根平行的光滑金属导轨，处在匀强磁场中，磁场方向垂直于导轨所在平面，导轨的一端与一电阻相连；具有一定质量的金属杆ab放在导轨上并与导轨垂直．现用一平行于导轨的恒力F拉杆ab，使它由静止开始向右运动．杆和导轨的电阻、感应电流产生的磁场均可不计．则（ ）分析：对金属杆进行受力分析，分析清楚金属杆的运动过程，然后由P=Fv判断拉力的功率如何变化，由牛顿第二定律判断加速度如何变化，从能量转化的角度分析焦耳热大小与合力的功间的关系．
解答：解：A、金属杆ab在运动过程中受到的安培力FB=BIL=B
L=B
L=
，
由牛顿第二定律可得，金属杆的加速度a=
=
-
，
金属杆从静止开始向右做加速运动，速度v逐渐增大，加速度a逐渐减小，
当拉力与安培力合力为零时，金属棒的加速度为零，金属棒做匀速直线运动，
即：金属棒的运动过程是：先做加速度逐渐减小的加速运动，后做匀速直线运动，
由P=Fv可知，拉力的功率先增大，后不变，故AB正确；
C、由动能定理可知，合力所做的功等于金属杆动能的变化量，不等于电阻上产生的焦耳热，
电阻上产生的焦耳热等于克服安培力所做的功，故C错误；
D、撤去拉力F后，金属杆在安培力作用下做减速运动，最后静止，故D错误；
故选AB．
| E |
| R |
| BLv |
| R |
| B2L2v |
| R |
由牛顿第二定律可得，金属杆的加速度a=
| F-FB |
| m |
| F |
| m |
| B2L2v |
| mR |
金属杆从静止开始向右做加速运动，速度v逐渐增大，加速度a逐渐减小，
当拉力与安培力合力为零时，金属棒的加速度为零，金属棒做匀速直线运动，
即：金属棒的运动过程是：先做加速度逐渐减小的加速运动，后做匀速直线运动，
由P=Fv可知，拉力的功率先增大，后不变，故AB正确；
C、由动能定理可知，合力所做的功等于金属杆动能的变化量，不等于电阻上产生的焦耳热，
电阻上产生的焦耳热等于克服安培力所做的功，故C错误；
D、撤去拉力F后，金属杆在安培力作用下做减速运动，最后静止，故D错误；
故选AB．
点评：对金属杆正确受力分析，分析清楚运动过程、从能量角度分析问题，是正确解题的关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
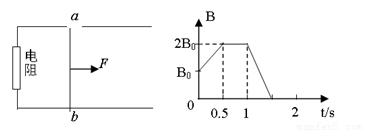
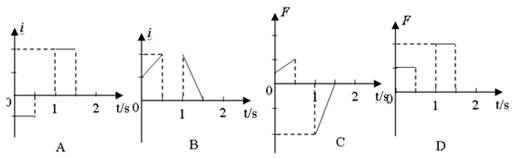
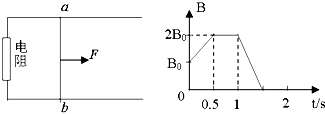如图所示，位于同一水平面内的，两根平行的光滑金属导轨，处在匀强磁场中，磁场方向垂直于导轨所在平面，导轨的一端与一电阻相连，具有一定质量的金属杆ab放在导轨上并与导轨垂直，当磁场的磁感应强度B随时间t如图变化时（规定垂直纸面向里的磁场方向为正），用一平行于导轨的力F向左或向右拉杆ab，使它保持静止．若规定由a→b方向通过杆的感应电流为正，向右的拉力为正，则能反映通过杆的感应电流I和拉力F随时间t变化的图线是（ ）
