题目内容
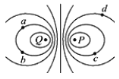
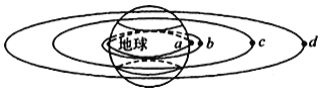
【题目】如图所示,a为放在地球赤道上随地球表面一起转动的物体,b为处于地面附近近地轨道上的卫星,c是地球同步卫星,d是高空探测卫星,若a、b、c、d的质量相同,地球表面附近的重力加速度为g。则下列说法正确的是( )
A.d是三颗卫星中动能最小,机械能最大的
B.c距离地面的高度不是一确定值
C.a和b的向心加速度都等于重力加速度g
D.a的角速度最大
【答案】A
【解析】
A.卫星做圆周运动万有引力提供向心力,由牛顿第二定律得:
![]()
卫星的动能:
![]()
三颗卫星中d的轨道半径最大,则d的动能最小,以无穷远处为零势能面,机械能:
![]()
d的轨道半径最大,d的机械能最大,故A正确;
B.c是同步卫星,同步卫星相对地面静止,c的轨道半径是一定的,c距离地面的是一确定值,故B错误;
C.同步卫星的周期必须与地球自转周期相同,角速度相同,则知a与c的角速度相同,根据a=ω2r知,a的向心加速度小于c的向心加速度。由牛顿第二定律得:
![]()
解得:
![]()
卫星的轨道半径越大,向心加速度越小,则同步卫星c的向心加速度小于b的向心加速度,而b的向心加速度约为g,故知a的向心加速度小于重力加速度g,故C错误;
D.万有引力提供向心力,由牛顿第二定律得:
![]()
解得:
![]()
由于rb<rc<rd,则ωb>ωc>ωd,a与c的角速度相等,则b的角速度最大,故D错误;

 名校课堂系列答案
名校课堂系列答案【题目】某课外活动小组使用如图所示的实验装置进行《验证机械能守恒定律》的实验,主要步骤:
A、用游标卡尺测量并记录小球直径d
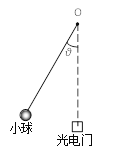
B、将小球用细线悬于O点,用刻度尺测量并记录悬点O到球心的距离l
C、将小球拉离竖直位置由静止释放,同时测量并记录细线与竖直方向的夹角θ
D、小球摆到最低点经过光电门,光电计时器(图中未画出)自动记录小球通过光电门的时间Δt
E、改变小球释放位置重复C、D多次
F、分析数据,验证机械能守恒定律
请回答下列问题:
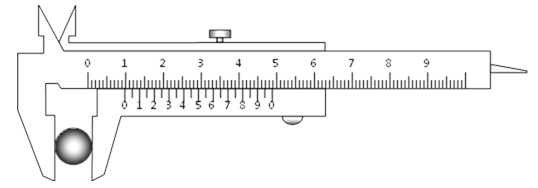
(1)步骤A中游标卡尺示数情况如下图所示,小球直径d=________mm
(2)实验记录如下表,请将表中数据补充完整(表中v是小球经过光电门的速度
θ | 10° | 20° | 30° | 40° | 50° | 60° |
cosθ | 0.98 | 0.94 | 0.87 | 0.77 | 0.64 | 0.50 |
Δt/ms | 18.0 | 9.0 | 6.0 | 4.6 | 3.7 | 3.1 |
v/ms-1 | 0.54 | 1.09 | ①_____ | 2.13 | 2.65 | 3.16 |
v 2/m2s-2 | 0.30 | 1.19 | ②_______ | 4.54 | 7.02 | 9.99 |
(3)某同学为了作出v 2- cosθ图像,根据记录表中的数据进行了部分描点,请补充完整并作出v 2- cosθ图像(______)
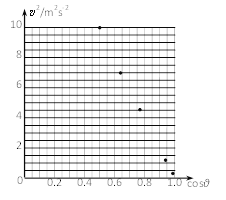
(4)实验完成后,某同学找不到记录的悬点O到球心的距离l了,请你帮助计算出这个数据l=____m (保留两位有效数字),已知当地重力加速度为9.8m/s2。