题目内容
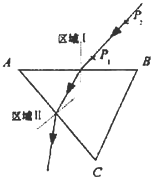
 如图所示,某同学用插针法测量等腰三棱镜的折射率.在区域Ⅰ内已插好两枚大头针P1、P2,在区域Ⅱ内可观察到大头针的像,再插大头针P3、P4,以挡住P1、P2的像.
如图所示,某同学用插针法测量等腰三棱镜的折射率.在区域Ⅰ内已插好两枚大头针P1、P2,在区域Ⅱ内可观察到大头针的像,再插大头针P3、P4,以挡住P1、P2的像.(1)请作出经过P1、P2、P3、P4的光路;
(2)若测得AB面上的入射角为θ1,折射角为θ2,请写出该介质全反射临界角的表达式;
(3)若测得该介质折射率为n,那么光波在介质中的传播速度是多少?光由空气进入介质前后,波长变化了多少?(已知入射光的频率为f)
分析:作出光路图,根据折射定律求出折射率的大小,从而根据sinC=
求出临界角的表达式.根据v=
求出光在介质中的传播速度,结合波长、频率、波速的关系,抓住频率不变,求出波长的变化量.
| 1 |
| n |
| c |
| n |
解答:解:(1)光路图如图所示.
(2)根据折射定律得,n=
,sinC=
=
临界角C=arcsin
(3)光在三棱镜中的传播速度 v=
波长 λ=
=
波长减小,减小量 △λ=λ0-λ=
-
=
?
.
答:(1)如图所示.
(2)该介质全反射临界角的表达式C=arcsin
.
(3)光波在介质中的传播速度是v=
,光由空气进入介质前后,波长变化了
?
.

(2)根据折射定律得,n=
| sinθ1 |
| sinθ2 |
| 1 |
| n |
| sinθ2 |
| sinθ1 |
临界角C=arcsin
| sinθ2 |
| sinθ1 |
(3)光在三棱镜中的传播速度 v=
| c |
| n |
波长 λ=
| v |
| f |
| c |
| nf |
波长减小,减小量 △λ=λ0-λ=
| c |
| f |
| c |
| nf |
| n-1 |
| n |
| c |
| f |
答:(1)如图所示.
(2)该介质全反射临界角的表达式C=arcsin
| sinθ2 |
| sinθ1 |
(3)光波在介质中的传播速度是v=
| c |
| n |
| n-1 |
| n |
| c |
| f |
点评:解决本题的关键掌握折射定律以及全反射的条件,以及知道波速、波长、频率的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
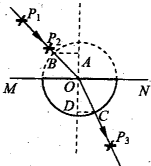
 如图所示,某同学用插针法测定一半圆形玻璃砖的折射率.在平铺的白纸上垂直纸面插大头针P1、P2确定入射光线,并让入射光线过圆心O,在玻璃砖(图中实线部分)另一侧垂直纸面插大头针P3,使P3挡住P1、P2的像,连接O P3.图中MN为分界面,虚线半圆与玻璃砖对称,B、C分别是入射光线、折射光线与圆的交点,AB、CD均垂直于法线并分别交法线于A、D点.
如图所示,某同学用插针法测定一半圆形玻璃砖的折射率.在平铺的白纸上垂直纸面插大头针P1、P2确定入射光线,并让入射光线过圆心O,在玻璃砖(图中实线部分)另一侧垂直纸面插大头针P3,使P3挡住P1、P2的像,连接O P3.图中MN为分界面,虚线半圆与玻璃砖对称,B、C分别是入射光线、折射光线与圆的交点,AB、CD均垂直于法线并分别交法线于A、D点. (1)如图所示,某同学用插针法测定一半圆形玻璃砖的折射率.在平铺的白纸上垂直纸面插大头针Pl、P2确定入射光线,并让入射光线过圆心O,在玻璃砖(图中实线部分)另一侧垂直纸面插大头针P3,使P3挡住P1、P2的像,连接OP3.图中MN为分界面,虚线半圆与玻璃砖对称,B、C分别是入射光线、折射光线与圆的交点,AB、CD均垂直于法线并分别交法线于A、D点.
(1)如图所示,某同学用插针法测定一半圆形玻璃砖的折射率.在平铺的白纸上垂直纸面插大头针Pl、P2确定入射光线,并让入射光线过圆心O,在玻璃砖(图中实线部分)另一侧垂直纸面插大头针P3,使P3挡住P1、P2的像,连接OP3.图中MN为分界面,虚线半圆与玻璃砖对称,B、C分别是入射光线、折射光线与圆的交点,AB、CD均垂直于法线并分别交法线于A、D点.
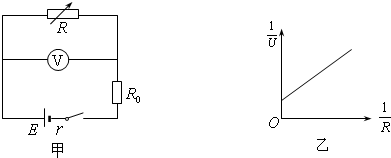
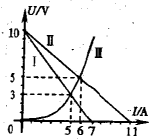 (1)如图所示,直线I、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,则电源1和电源2的内阻之比为
(1)如图所示,直线I、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,则电源1和电源2的内阻之比为
 示,某同学用插针法测定一半圆形玻璃砖的折射率,在平铺的白纸上垂直纸面插大头针P1、P2确定入射光线,
示,某同学用插针法测定一半圆形玻璃砖的折射率,在平铺的白纸上垂直纸面插大头针P1、P2确定入射光线, (1)①假设有两颗人造卫星正环绕月球做匀速圆周运动,甲卫星在近月轨道上运行(忽略离月球表面的高度),周期为T,乙卫星在距离月球表面h高度的轨道上运行,周期为
(1)①假设有两颗人造卫星正环绕月球做匀速圆周运动,甲卫星在近月轨道上运行(忽略离月球表面的高度),周期为T,乙卫星在距离月球表面h高度的轨道上运行,周期为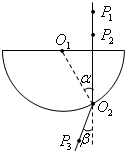 大头针P1、P2的连线与半圆的直径垂直,与圆弧的交点为O2.
大头针P1、P2的连线与半圆的直径垂直,与圆弧的交点为O2.