题目内容
18.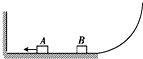 如图所示,竖直平面内的光滑水平轨道的左边有一墙壁,右边与一个足够高的光滑圆弧轨道平滑相连,木块A、B静置于光滑水平轨道上,A、B的质量分别为1.5kg和0.5kg.现让A以6m/s的速度水平向左运动,之后与墙壁碰撞,碰撞的时间为0.3s,碰后的速度大小变为4m/s.若A与B碰撞后会立即粘在一起运动,g取10m/s2,求:
如图所示,竖直平面内的光滑水平轨道的左边有一墙壁,右边与一个足够高的光滑圆弧轨道平滑相连,木块A、B静置于光滑水平轨道上,A、B的质量分别为1.5kg和0.5kg.现让A以6m/s的速度水平向左运动,之后与墙壁碰撞,碰撞的时间为0.3s,碰后的速度大小变为4m/s.若A与B碰撞后会立即粘在一起运动,g取10m/s2,求:(1)在A与墙壁碰撞的过程中,墙壁对A的平均作用力的大小.
(2)A、B滑上圆弧轨道的最大高度.
分析 (1)A碰撞墙壁过程,应用动量定理可以求出作用力.
(2)A、B碰撞过程系统动量守恒、机械能守恒,由动量守恒定律与机械能守恒定律可以求出最大高度.
解答 解:(1)设水平向右为正方向,当A与墙壁碰撞时,
由动量定理得:Ft=mAv′1-mA•(-v1),
解得:F=50N.
(2)设碰撞后A、B的共同速度为v,以向右为正方向,
由动量守恒定律得:mAv′1=(mA+mB)v,
A、B在光滑圆形轨道上滑动时,机械能守恒,
由机械能守恒定律得:$\frac{1}{2}$(mA+mB)v2=(mA+mB)gh,
解得:h=0.45m;
答:(1)在A与墙壁碰撞的过程中,墙壁对A的平均作用力的大小为50N;
(2)A、B滑上圆弧轨道的最大高度为0.45m
点评 本题考查了求作用力、高度问题,分析清楚物体运动过程,正确应用动量定理、动量守恒定律、机械能守恒定律即可正确解题.

练习册系列答案
相关题目
6.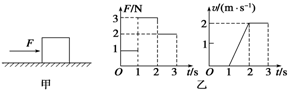 如图甲所示,物体受到水平推力F的作用,在粗糙水平面上做直线运动.通过力传感器和速度传感器监测到推力F和物体速度v随时间t变化的规律如图乙所示.重力加速度g=10m/s2.则( )
如图甲所示,物体受到水平推力F的作用,在粗糙水平面上做直线运动.通过力传感器和速度传感器监测到推力F和物体速度v随时间t变化的规律如图乙所示.重力加速度g=10m/s2.则( )
 如图甲所示,物体受到水平推力F的作用,在粗糙水平面上做直线运动.通过力传感器和速度传感器监测到推力F和物体速度v随时间t变化的规律如图乙所示.重力加速度g=10m/s2.则( )
如图甲所示,物体受到水平推力F的作用,在粗糙水平面上做直线运动.通过力传感器和速度传感器监测到推力F和物体速度v随时间t变化的规律如图乙所示.重力加速度g=10m/s2.则( )| A. | 物体的质量m=0.5kg | |
| B. | 第2s内物体克服摩擦力做的功W=2J | |
| C. | 物体与水平面间的动摩擦因数μ=0.4 | |
| D. | 前2 s内推力F做功的平均功率$\overline{P}$=1 W |
13.在研究下列问题中,能够把研究对象看作质点的是( )
| A. | 研究地球的自转 | |
| B. | 研究地球绕太阳的公转 | |
| C. | 研究一列火车通过路边一根电线杆所用的时间 | |
| D. | 研究2012年伦敦奥运会上我国女单选手李晓霞乒乓球的旋转 |