题目内容
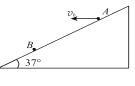
【题目】如图所示,AB是倾角![]() 为450的直轨道,CD是半径R=0.4m的圆弧轨道,它们通过一段曲面BC平滑相接,整个轨道处于竖直平面内,且处处光滑。一个质量m=1kg的物体(可视为质点),从高H的地方由静止释放,结果它从圆弧最高点D点飞出,垂直斜面击中P点。已知P点与圆弧的圆心O等高,g取10m/s2。求:
为450的直轨道,CD是半径R=0.4m的圆弧轨道,它们通过一段曲面BC平滑相接,整个轨道处于竖直平面内,且处处光滑。一个质量m=1kg的物体(可视为质点),从高H的地方由静止释放,结果它从圆弧最高点D点飞出,垂直斜面击中P点。已知P点与圆弧的圆心O等高,g取10m/s2。求:

(1)物体击中P点前瞬间的速度。
(2)物体在C点的速度为多少(结果可用根式表示)。
(3)物体静止释放时的高度H。
【答案】(1) ![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)物体从D点运动到P点做平抛运动,竖直方向做自由落体运动,
则竖直方向有:2gR=vy2;
解得: ![]()
根据几何关系得:物体击中P点的速度![]()
(2)从C到P的过程,根据机械能守恒定律得: ![]()
解得: ![]()
(3)物体从A到P的过程中,根据机械能守恒定律得: ![]()
解得:H=1.2m

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目