题目内容
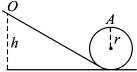
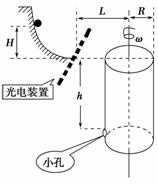
如图所示,小球从光滑的圆弧轨道下滑至水平轨道末端时,光电装置被触动,控制电路会使转筒立刻以某一角速度匀速连续转动起来。转筒的底面半径为R,已知轨道末端与转筒上部相平,与转筒的转轴距离为L,且与转筒侧壁上的小孔的高度差为h;开始时转筒静止,且小孔正对着轨道方向。现让一小球从圆弧轨道上的某处无初速滑下,若正好能钻入转筒的小孔(小孔比小球略大,小球视为质点,不计空气阻力,重力加速度为g),求:
(1)小球从圆弧轨道上释放时的高度H;
(2)转筒转动的角速度ω。
解:(1)设小球离开轨道进入小孔的时间为t,则由平抛运动规律得
h=![]() gt2
gt2
L-R=v0t
小球在轨道上运动过程中机械能守恒,故有mgH=![]() mv02
mv02
联立解得:t=![]()
H=![]() 。
。
(2)在小球做平抛运动的时间内,圆筒必须恰好转整数转,小球才能钻进小孔,即
ωt=2nπ(n=1,2,3,…)
所以ω=nπ![]() (n=1,2,3,…)。
(n=1,2,3,…)。

练习册系列答案
相关题目
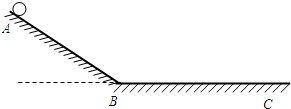 如图所示,小球从光滑斜面上的A点由静止开始匀加速下滑,经过B点后进入水平面(设经过B点前后速度大小不变)作匀减速运动,最后停在C点.每隔0.2s钟通过速度传感器测量小球的瞬时速度,下表给出了部分测量数据.(重力加速度g=10m/s2)求:
如图所示,小球从光滑斜面上的A点由静止开始匀加速下滑,经过B点后进入水平面(设经过B点前后速度大小不变)作匀减速运动,最后停在C点.每隔0.2s钟通过速度传感器测量小球的瞬时速度,下表给出了部分测量数据.(重力加速度g=10m/s2)求:
| t(s) | 0.0 | 0.2 | 0.4 | … | 1.2 | 1.4 | … |
| v(m/s) | 0.0 | 1.0 | 2.0 | … | 1.1 | 0.7 | … |
(2)小球在最初0.4s内的位移?
(3)小球下滑过程中的最大速度.
 (2011?抚州模拟)如图所示,小球从光滑的圆弧轨道下滑至水平轨道末端时,光电装置被触动,控制电路会使转筒立刻以某一角速度匀速连续转动起来.转筒的底面半径为R,已知轨道末端与转筒上部相平,与转筒的转轴距离为L,且与转筒侧壁上的小孔的高度差为h;开始时转筒静止,且小孔正对着轨道方向.现让一小球从圆弧轨道上的某处无初速滑下,若正好能钻入转筒的小孔(小孔比小球略大,小球视为质点,不计空气阻力,重力加速度为g),求:
(2011?抚州模拟)如图所示,小球从光滑的圆弧轨道下滑至水平轨道末端时,光电装置被触动,控制电路会使转筒立刻以某一角速度匀速连续转动起来.转筒的底面半径为R,已知轨道末端与转筒上部相平,与转筒的转轴距离为L,且与转筒侧壁上的小孔的高度差为h;开始时转筒静止,且小孔正对着轨道方向.现让一小球从圆弧轨道上的某处无初速滑下,若正好能钻入转筒的小孔(小孔比小球略大,小球视为质点,不计空气阻力,重力加速度为g),求: 如图所示,小球从光滑斜面上的A点由静止开始匀加速下滑,经过B点后进入水平面(设经过B点前后速度大小不变)作匀减速运动,最后停在C点.每隔0.2s钟通过速度传感器测量小球的瞬时速度,下表给出了部分测量数据.(重力加速度g=10m/s2)求:
如图所示,小球从光滑斜面上的A点由静止开始匀加速下滑,经过B点后进入水平面(设经过B点前后速度大小不变)作匀减速运动,最后停在C点.每隔0.2s钟通过速度传感器测量小球的瞬时速度,下表给出了部分测量数据.(重力加速度g=10m/s2)求: