题目内容
8.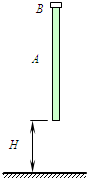 如图所示,粗细均匀的圆木棒A下端离地面高H,上端套着一个细环B.A和B的质量均为m,A和B间的滑动摩擦力为f,且f<mg.用手控制A和B使它们从静止开始自由下落.当A与地面碰撞后,A以碰撞地面时的速度大小竖直向上运动,与地面发生碰撞时间极短,空气阻力不计,运动过程中A始终呈竖直状态.求:若A再次着地前B不脱离A,A的长度应满足什么条件?
如图所示,粗细均匀的圆木棒A下端离地面高H,上端套着一个细环B.A和B的质量均为m,A和B间的滑动摩擦力为f,且f<mg.用手控制A和B使它们从静止开始自由下落.当A与地面碰撞后,A以碰撞地面时的速度大小竖直向上运动,与地面发生碰撞时间极短,空气阻力不计,运动过程中A始终呈竖直状态.求:若A再次着地前B不脱离A,A的长度应满足什么条件?
分析 刚开始棒和环一起向下做自由落体运动,求出棒落地时的速度,根据牛顿第二定律求出木棒弹起竖直上升过程中木棒和环的加速度,而环在木棒上升及下落的全过程中一直处于加速运动状态,所以木棒从向上弹起到再次着地的过程中,棒与环的加速度均保持不变,根据运动学基本公式求出棒再次着地时的时间,从而求出这段时间内环运动的位移即可棒的最小长度.
解答 解:设木棒着地时的速度为v0,因为木棒和环一起自由下落,则
${v}_{0}=\sqrt{2gH}$,
木棒弹起竖直上升过程中,根据牛顿第二定律得:
对木棒:f+mg=ma1,
解得:${a}_{1}=\frac{f+mg}{m}$,方向竖直向下,
对环:mg-f=ma2
解得:${a}_{2}=\frac{mg-f}{m}$,方向竖直向下,
可见,环在木棒上升及下落的全过程中一直处于加速运动状态,所以木棒从向上弹起到再次着地的过程中,棒与环的加速度均保持不变,
木棒再空中运动的时间为t=$\frac{2{v}_{0}}{{a}_{1}}$,
再这段时间内,环运动的位移为x=${v}_{0}t+\frac{1}{2}a{t}^{2}$,
要使环不碰地面,则要求木棒的长度不小于x,即L≥x,
解得:L≥$\frac{8{m}^{2}{g}^{2}H}{(mg+f)^{2}}$
答:若A再次着地前B不脱离A,A的长度应满足L≥$\frac{8{m}^{2}{g}^{2}H}{(mg+f)^{2}}$.
点评 本题主要考查了牛顿第二定律以及运动学基本公式的直接应用,要求同学们能正确分析棒和环的运动情况,知道棒和环的运动时间相等,再抓住位移关系求解,难度适中.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
3.作用在同一个物体上的下列几组共点力中,合力可能为零的有( )
| A. | 2N、3N、6 N | B. | 1 N、1 N、1 N | C. | 4 N、6 N、11 N | D. | 5 N、900 N、903 N |
3.如图所示,木板置于水平地面上,其上物块A被水平绳子拴接在左端墙上,将木板水平向右匀速抽出的过程中绳子的拉力为F;现将木板水平向右加速抽出,则此过程中绳子的拉力( )

| A. | 等于F | B. | 小于F | C. | 大于F | D. | 无法确定 |
13.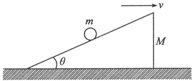 如图所示,质量为M、倾角为θ的斜劈在粗糙水平面上以一定的初速度向右滑动,在此过程中,质量为m的光滑小球在斜面上恰好与斜劈保持相对静止.已知斜劈与地面的动摩擦因数是μ,重力加速度为g,则下列说法正确的是( )
如图所示,质量为M、倾角为θ的斜劈在粗糙水平面上以一定的初速度向右滑动,在此过程中,质量为m的光滑小球在斜面上恰好与斜劈保持相对静止.已知斜劈与地面的动摩擦因数是μ,重力加速度为g,则下列说法正确的是( )
 如图所示,质量为M、倾角为θ的斜劈在粗糙水平面上以一定的初速度向右滑动,在此过程中,质量为m的光滑小球在斜面上恰好与斜劈保持相对静止.已知斜劈与地面的动摩擦因数是μ,重力加速度为g,则下列说法正确的是( )
如图所示,质量为M、倾角为θ的斜劈在粗糙水平面上以一定的初速度向右滑动,在此过程中,质量为m的光滑小球在斜面上恰好与斜劈保持相对静止.已知斜劈与地面的动摩擦因数是μ,重力加速度为g,则下列说法正确的是( )| A. | 小球与斜面间的压力大小是mgcosθ | B. | 小球与斜面的加速度大小是gsinθ | ||
| C. | 地面对斜劈的支持力大小等于(M+m)g | D. | 地面与斜劈间的动摩擦因数μ=tanθ |
17. 如图所示,在车厢顶部用OA、OB两根等长的细绳悬挂质量为m的小球,车静止时两细绳与竖直方向的夹角均为θ,当车处于向右的运动状态时,小球相对车厢的位置没有变化,则车向右运动时下列说法正确的是( )
如图所示,在车厢顶部用OA、OB两根等长的细绳悬挂质量为m的小球,车静止时两细绳与竖直方向的夹角均为θ,当车处于向右的运动状态时,小球相对车厢的位置没有变化,则车向右运动时下列说法正确的是( )
 如图所示,在车厢顶部用OA、OB两根等长的细绳悬挂质量为m的小球,车静止时两细绳与竖直方向的夹角均为θ,当车处于向右的运动状态时,小球相对车厢的位置没有变化,则车向右运动时下列说法正确的是( )
如图所示,在车厢顶部用OA、OB两根等长的细绳悬挂质量为m的小球,车静止时两细绳与竖直方向的夹角均为θ,当车处于向右的运动状态时,小球相对车厢的位置没有变化,则车向右运动时下列说法正确的是( )| A. | 两绳的张力大小一定相等 | B. | OB绳的张力可能大于OA绳的张力 | ||
| C. | 车的加速度大小可能等于gtanθ | D. | 车的加速度大小可能等于2gtanθ |
18.如图所示,物体静置于水平桌面上,下列关于弹力的说法中正确的是( )

| A. | 桌面受到的压力就是物体的重力 | |
| B. | 桌面受到的压力是由于它本身发生了微小形变而产生的 | |
| C. | 桌面由于发生了微小形变而对物体产生了垂直于桌面的支持力 | |
| D. | 物体由于发生了微小形变而对物体产生了垂直于桌面的压力 |