题目内容
2. 如图所示,质量均为m的物块A和B用劲度系数为k的轻弹簧连接起来;将它们悬于空中静止,弹簧处于原长状态,A距地面高度h,现同时释放两物块,A与地面碰撞速度立即变为零,由于B的反弹,使A刚好能离开地面.若将B物块换为质量为3m的物块C(图中未画出),仍将它们悬于空中静止且弹簧为原长,A距地面高度仍为h,再同时释放两物块,A与地面碰撞后仍立即变为零.求:当A刚要离开地面时物块C的速度.
如图所示,质量均为m的物块A和B用劲度系数为k的轻弹簧连接起来;将它们悬于空中静止,弹簧处于原长状态,A距地面高度h,现同时释放两物块,A与地面碰撞速度立即变为零,由于B的反弹,使A刚好能离开地面.若将B物块换为质量为3m的物块C(图中未画出),仍将它们悬于空中静止且弹簧为原长,A距地面高度仍为h,再同时释放两物块,A与地面碰撞后仍立即变为零.求:当A刚要离开地面时物块C的速度.
分析 由题意,当A与地面相碰瞬间,弹簧刚好处于原长,由机械能守恒即可求出物体的速度;当A刚好要离开地面时,此时B的速度为零,B的动能转化为B的重力势能和弹簧的弹性势能;将B物块换为质量为3m的物块C,A刚好要离开地面时,此时C的速度不为零,B的动能转化为B的动能、重力势能和弹簧的弹性势能,然后又机械能守恒定律即可求解.
解答 解:当A与地面相碰瞬间,弹簧刚好处于原长
此时${v_B}=\sqrt{2gh}$…①
当A刚好要离开地面时,此时B的速度为零,设此时弹簧的伸长量为X1,有
mg=kX1…②
从A与地面碰撞后到A刚好能离开地面过程中,由能量守恒:$\frac{1}{2}mv_B^2=mg{X_1}+{E_{p1}}$…③
把B换成C弹簧处于原长时,C的速度${v_c}=\sqrt{2gh}$…④
当A刚好离地时有:
mg=Kx2…⑤
从A与地面碰撞后到A刚好能离开地面过程中,由能量守恒:$\frac{1}{2}(3m)v_c^2=(3m)g{X_2}+{E_{o2}}+\frac{1}{2}(3m)v_1^2$…⑥
X1=X2 Ep1=Ep2…⑦
得${v_1}=2\sqrt{\frac{g(kh-mg)}{2k}}$…⑧
答:A刚要离开地面时物块C的速度是$2\sqrt{\frac{g(kh-mg)}{2k}}$.
点评 本题主要考查了机械能守恒定律的应用,要求同学们能正确分析物体的运动情况,选择正确的过程及研究对象,区分两种情况下能量转化的差别.

练习册系列答案
相关题目
13.科学的研究方法促进了人们对事物本质和规律的认识,以下说法中正确的是( )
| A. | 法拉第在研究电磁感应现象时,利用了理想实验的方法 | |
| B. | 螺旋测微器的设计主要采用了放大法 | |
| C. | 确定交流电的有效值应用了控制变量法 | |
| D. | 库仑对点电荷间相互作用的研究采用了等效替代法 |
10. 在一本科幻小说中,一名旅客乘搭升降机以恒速度抵达太空站,升降机并是垂直的,而且地球自传的影响可以忽略不计,在下列各个线图中,哪一个最能表达旅客的表现重量W随离地高度h的变化?( )
在一本科幻小说中,一名旅客乘搭升降机以恒速度抵达太空站,升降机并是垂直的,而且地球自传的影响可以忽略不计,在下列各个线图中,哪一个最能表达旅客的表现重量W随离地高度h的变化?( )
 在一本科幻小说中,一名旅客乘搭升降机以恒速度抵达太空站,升降机并是垂直的,而且地球自传的影响可以忽略不计,在下列各个线图中,哪一个最能表达旅客的表现重量W随离地高度h的变化?( )
在一本科幻小说中,一名旅客乘搭升降机以恒速度抵达太空站,升降机并是垂直的,而且地球自传的影响可以忽略不计,在下列各个线图中,哪一个最能表达旅客的表现重量W随离地高度h的变化?( )| A. | 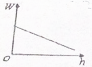 | B. |  | C. |  | D. |  |
7.在某些恒星内,三个α粒子结合成一个${\;}_{6}^{12}$C核,${\;}_{6}^{12}$C的质量为12.0000u,${\;}_{2}^{4}$He的质量为4.0026u,已知lu=1.6606×10-27kg,c=3.00×108m/s.则下列表述正确的是( )
| A. | 该反应属原子核的人工转变,反应中释放的核能为7.266MeV | |
| B. | 该反应属原子核的裂变反应,质量亏损为0.0078u | |
| C. | 该反应属原子核的聚变反应,反应中释放的核能约为1.16×10-10J | |
| D. | 该反应属热核反应,其中${\;}_{6}^{12}$C核子的平均质量小于${\;}_{2}^{4}$He核子的平均质量 |
11. 如图所示,AB两物体在同一直线上运动,当它们相距s=7m时,A在水平拉力和摩擦力的作用下,正以4m/s的速度向右做匀速运动,而物体B此时速度为10m/s,方向向右,它在摩擦力作用下做匀减速运动,加速度大小为2m/s2,则A追上B用的时间为( )
如图所示,AB两物体在同一直线上运动,当它们相距s=7m时,A在水平拉力和摩擦力的作用下,正以4m/s的速度向右做匀速运动,而物体B此时速度为10m/s,方向向右,它在摩擦力作用下做匀减速运动,加速度大小为2m/s2,则A追上B用的时间为( )
 如图所示,AB两物体在同一直线上运动,当它们相距s=7m时,A在水平拉力和摩擦力的作用下,正以4m/s的速度向右做匀速运动,而物体B此时速度为10m/s,方向向右,它在摩擦力作用下做匀减速运动,加速度大小为2m/s2,则A追上B用的时间为( )
如图所示,AB两物体在同一直线上运动,当它们相距s=7m时,A在水平拉力和摩擦力的作用下,正以4m/s的速度向右做匀速运动,而物体B此时速度为10m/s,方向向右,它在摩擦力作用下做匀减速运动,加速度大小为2m/s2,则A追上B用的时间为( )| A. | 7s | B. | 8s | C. | 9s | D. | 10s |
12. 某工地上,一架起重机将放在地面的一个箱子吊起.箱子在起重机钢绳的作用下由静止开始竖直向上运动,运动过程中箱子的机械能E与其位移x关系的图象如图所示,其中O~x1过程的图线为曲线,x1~x2过程的图线为直线.根据图象可知( )
某工地上,一架起重机将放在地面的一个箱子吊起.箱子在起重机钢绳的作用下由静止开始竖直向上运动,运动过程中箱子的机械能E与其位移x关系的图象如图所示,其中O~x1过程的图线为曲线,x1~x2过程的图线为直线.根据图象可知( )
 某工地上,一架起重机将放在地面的一个箱子吊起.箱子在起重机钢绳的作用下由静止开始竖直向上运动,运动过程中箱子的机械能E与其位移x关系的图象如图所示,其中O~x1过程的图线为曲线,x1~x2过程的图线为直线.根据图象可知( )
某工地上,一架起重机将放在地面的一个箱子吊起.箱子在起重机钢绳的作用下由静止开始竖直向上运动,运动过程中箱子的机械能E与其位移x关系的图象如图所示,其中O~x1过程的图线为曲线,x1~x2过程的图线为直线.根据图象可知( )| A. | O~x1过程中钢绳的拉力逐渐增大 | |
| B. | O~x1过程中箱子的动能一直增加 | |
| C. | x1~x2过程中钢绳的拉力一直不变 | |
| D. | x1~x2过程中起重机的输出功率一直增大 |
 如图所示,在平静的水面下有一点光源S正在以速度V匀速上浮,开始时点光源到水面的距离为H,水对该光源发出的单色光的折射率为n.请解答下列问题:
如图所示,在平静的水面下有一点光源S正在以速度V匀速上浮,开始时点光源到水面的距离为H,水对该光源发出的单色光的折射率为n.请解答下列问题: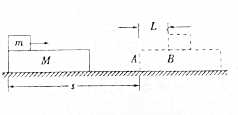 质量为M的长木板放在光滑的水平面上(如图所示).一个质量为m的滑块以某一速度沿木板上表面从A点滑至B点,在木板上前进了s,若滑块与木板间的动摩擦因数为μ,求:
质量为M的长木板放在光滑的水平面上(如图所示).一个质量为m的滑块以某一速度沿木板上表面从A点滑至B点,在木板上前进了s,若滑块与木板间的动摩擦因数为μ,求: 现有一块灵敏电流表A1,量程为200 μA,内阻R1约l000Ω,吴丽同学要精确测定其内阻,实验室提供的器材有:
现有一块灵敏电流表A1,量程为200 μA,内阻R1约l000Ω,吴丽同学要精确测定其内阻,实验室提供的器材有: