题目内容
14.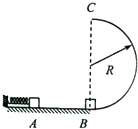 如图,光滑水平面AB与竖直面内的半圆形轨道BC相切于B点,半圆轨道半径为R,质量为m的木块从A处由弹簧沿AB方向弹出,当它经过B点时对半圆轨道的压力是其重力的8倍,到达顶点C时对轨道的压力为0,已知重力加速度为g,不计空气阻力,求:
如图,光滑水平面AB与竖直面内的半圆形轨道BC相切于B点,半圆轨道半径为R,质量为m的木块从A处由弹簧沿AB方向弹出,当它经过B点时对半圆轨道的压力是其重力的8倍,到达顶点C时对轨道的压力为0,已知重力加速度为g,不计空气阻力,求:(1)木块经过B点时的速度大小v;
(2)木块从B到C过程中.克服摩擦力做的功W.
分析 (1)在B点由牛顿第二定律求的速度;
(2)物体恰好通过C点,在C点由牛顿第二定律求的C点速度,从B到C根据动能定理求得摩擦力做功
解答 解:(1)在B点由牛顿第二定律可得${F}_{N}-mg=\frac{{mv}_{B}^{2}}{R}$
由牛顿第三定律可得FN=8mg
联立解得${v}_{B}=\sqrt{7gR}$
(2)在C点由牛顿第二定律可得mg=$\frac{{mv}_{C}^{2}}{R}$
从B到C由动能定理可得$-mg•2R-W=\frac{1}{2}{mv}_{C}^{2}-\frac{1}{2}{mv}_{B}^{2}$
联立解得W=mgR
答:(1)木块经过B点时的速度大小v为$\sqrt{7gR}$;
(2)木块从B到C过程中.克服摩擦力做的功W为mgR
点评 解答本题首先应明确物体运动的三个过程,第一过程弹力做功增加了物体的动能;第二过程做竖直面上的圆周运动,要注意临界条件的应用

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
5.关于弹力,下列说法正确的是( )
| A. | 相互接触的物体间必定有弹力的作用 | |
| B. | 物体对桌面的压力就是木块受的重力,施力物体是地球 | |
| C. | 物体对桌面产生的压力是物体发生微小形变而产生的 | |
| D. | 在桌面上的物体对桌面产生的压力就是物体的重力 |
2.以下关于电场线的说法中,正确的是( )
| A. | 电场线上某点的切线方向,就是正电荷在该点所受的电场力方向 | |
| B. | 正电荷从静止开始释放,仅在电场力作用下,一定沿电场线运动 | |
| C. | 电场线紧密的地方,电势越高 | |
| D. | 电场线是人们为了形象直观地描述电场而提出的,实际并不存在 |
9.一公共汽车以v0=10m/s行驶,司机从后视镜中发现一人在车后以v=4m/s的速度追赶汽车,若人与汽车相距x=7m,汽车司机立即刹车只在摩擦力作用下做匀减速运动,加速度大小为a=2m/s2,那么人追上汽车所用的时间为( )
| A. | 7s | B. | 8s | C. | 9s | D. | 10s |
19. 如图是某定值电阻R的I-U图象,图中a=45°,下列说法正确的是( )
如图是某定值电阻R的I-U图象,图中a=45°,下列说法正确的是( )
 如图是某定值电阻R的I-U图象,图中a=45°,下列说法正确的是( )
如图是某定值电阻R的I-U图象,图中a=45°,下列说法正确的是( )| A. | 电阻R=0.5Ω | |
| B. | 因I-U图象的斜率表示电阻的倒数,故R=$\frac{1}{tan45°}$=1.0Ω | |
| C. | 通过电阻的电流与电阻两端电压成正比 | |
| D. | 在R两端加上5V的电压时,1秒钟通过电阻横截面的电荷量是2.5C |
3. 如图所示,虚线a、b、c表示电场中的三个等势面,相邻等势面间的电势差相等,实线为一个带正电的质点仅在电场力作用下,通过该区域的运动轨迹,P、Q是轨迹上的两点.下列说法中正确的是( )
如图所示,虚线a、b、c表示电场中的三个等势面,相邻等势面间的电势差相等,实线为一个带正电的质点仅在电场力作用下,通过该区域的运动轨迹,P、Q是轨迹上的两点.下列说法中正确的是( )
 如图所示,虚线a、b、c表示电场中的三个等势面,相邻等势面间的电势差相等,实线为一个带正电的质点仅在电场力作用下,通过该区域的运动轨迹,P、Q是轨迹上的两点.下列说法中正确的是( )
如图所示,虚线a、b、c表示电场中的三个等势面,相邻等势面间的电势差相等,实线为一个带正电的质点仅在电场力作用下,通过该区域的运动轨迹,P、Q是轨迹上的两点.下列说法中正确的是( )| A. | 三个等势面中,等势面a的电势最高 | |
| B. | 带电质点通过P点时的电势能比通过Q点时的小 | |
| C. | 带电质点通过P点时的动能比通过Q点时的小 | |
| D. | 带电质点通过P点时的加速度比通过Q点时的大 |
4.把一块铅和一块金的接触面磨平磨光后紧紧压在一起,若干年后发现金中有铅,铅中有金.对此现象说法正确的是( )
| A. | 属于扩散现象,原因是金分子和铅分子的相互吸引 | |
| B. | 属于扩散现象,原因是金分子和铅分子的热运动 | |
| C. | 属于布朗运动,小金粒进入铅块中,小铅粒进入金块 | |
| D. | 属于布朗运动,由于外界压力使小金粒、小铅粒彼此进入对方 |
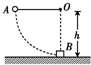 如图所示,小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h.质量是小球的2倍的物块B,置于粗糙的水平面上且位于O点的正下方,物块B与水平面间的动摩擦因数为μ.现拉动小球使线水平伸直,由静止开始释放小球,运动到最低点时与物块发生弹性正碰.小球与物块均视为质点,不计空气阻力,重力加速度为g.求:
如图所示,小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h.质量是小球的2倍的物块B,置于粗糙的水平面上且位于O点的正下方,物块B与水平面间的动摩擦因数为μ.现拉动小球使线水平伸直,由静止开始释放小球,运动到最低点时与物块发生弹性正碰.小球与物块均视为质点,不计空气阻力,重力加速度为g.求: