题目内容
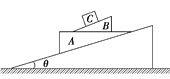
【题目】质量为mB=2 kg的足够长木板B静止于光滑水平地面上,在其右侧地面上固定一竖直挡板,质量为mA=6 kg的物块A停在B的左端,质量为mC=2 kg的小球C用长为L=0.8 m的轻绳悬挂在固定点O,绳能承受的最大拉力是小球C重力的9倍。现将小球C及轻绳拉直至水平位置后由静止释放,小球C在最低点与A发生正碰,碰撞时间极短,碰后小球C反弹瞬间绳刚好被拉断。已知A、B间的动摩擦因数![]() ,木板B与挡板发生弹性碰撞,且B与挡板碰撞前已与A共速,物块与小球均可视为质点,不计空气阻力,取g=10 m/s2。求:
,木板B与挡板发生弹性碰撞,且B与挡板碰撞前已与A共速,物块与小球均可视为质点,不计空气阻力,取g=10 m/s2。求:

(1)小球C与A撞后瞬间,A的速度;
(2)在木板B与挡板第一次碰撞前,A相对B滑动的位移;
(3)在A、B运动的整个过程中,A相对B的总位移及B向左运动的总路程。
【答案】(1)4m/s;(2)2m;(3)8m,2m
【解析】
(1)对小球C下摆的过程,应用动能定理求出小球与A碰撞前瞬间的速度,再向心力公式求得小球C反弹上升的初速度,即与A碰后的速度,根据动量守恒定律求解A的速度;
(2)运用动量守恒和能量守恒求出A相对B滑动的位移;
(3)仔细分析整个运动过程,利用用动量和能量守恒、同时结合数学的等比数列进行接题;
(1)小球C下摆的过程中,根据动能定理有:![]()
代入数据解得碰前C的速度为:![]() ,方向水中向右
,方向水中向右
设小球C与A碰撞后反弹的速度为![]() ,根据牛顿第二定律可知:
,根据牛顿第二定律可知:
![]() ,其中
,其中![]() ,联立可以得到:
,联立可以得到:![]() ,方向水中向左
,方向水中向左
在小球C与A碰撞瞬间动量守恒,以水平向右为正方向,则:![]()
代入数值可以得到:![]() ,方向水中向右;
,方向水中向右;
(2)由题可知,木板B与挡板发生碰撞前,A与B已经共速,设速度为![]()
以A、B为系统,以水平向右为正方向,根据动量守恒:![]()
代入数据可以得到:![]() ,方向水平向右
,方向水平向右
设第一碰撞前,A、B相对位移为![]() ,则根据能量守恒可以得到:
,则根据能量守恒可以得到:
![]()
代入数值可以得到:![]() ;
;
(3)由题可知木板B与挡板发生弹性碰撞,则碰后木板B以原速率反弹,而A仍以原速度前进,即A减速前进,木板B先向右减速然后向左加速,当再次A共速后与挡板再次发生碰撞,接着再次重复上述过程,直到最终二者动停止
设整个过程中A相对于B的总位移为![]() ,则根据能量守恒可知:
,则根据能量守恒可知:![]()
代入数据可以得到:![]() ;
;
由上面分析可知:第一次碰撞:![]() ,
,![]()
反弹之后再次共速:![]() ,则:
,则:![]()
第二次碰撞,反弹、共速:![]() ,则:
,则:![]()
第三次碰撞,反弹、共速:![]() ,则:
,则:![]()
…
每次与挡板碰撞之后,木板B都是先向左做减速运动到零之后,再反向向右加速
只研究木板B向左减速过程,只有A对B的摩擦力做负功,设木板B向左减速运动的总路程为![]() ,则根据动能定理可以得到:
,则根据动能定理可以得到:![]()
根据数学等比数列知识可以得到:![]() 。
。

 阅读快车系列答案
阅读快车系列答案