题目内容
8.图中实线是一列正弦波在某时刻t的波形图线,虚线是(t+△t)后的波形图线,波沿x轴传播,且已知△t=0.2s,求: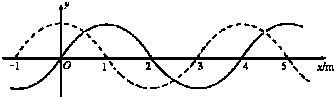
(1)这列波的波长;
(2)这列波可能的传播速度.
(3)若T<△t<3T,波速多大?
分析 (1)由图直接读出波长.
(2)波可能向右传播,也可能向左传播,向右传播的最短距离为1m,向左传播的最短距离为3m.考虑波的周期性,分别写出向左和向右传播距离的通项,由公式v=$\frac{x}{t}$求出波速的表达式.
(3)若T<△t<3T,则n=1,2,由上式求出波速.
解答 解:(1)这列波的波长为4m.
(2)波向左传播时传播的距离为 x=(n+$\frac{3}{4}$)λ=(4n+3)m,(n=0,1,2…),波速为v=$\frac{x}{t}$=$\frac{4n+3}{0.2}$=(20n+15)m/s;
向右传播时传播的距离为 x=(n+$\frac{1}{4}$)λ=(4n+1)m(m),(n=0,1,2…),波速为 v=$\frac{x}{t}$=(20n+5)m/s,(n=0,1,2…)
(3)若T<△t<3T,则n=1,2,代入上式可得:若波向左传播时波速为35m/s,55m/s;若波向右传播时波速为25m/s,45m/s;
答:
(1)这列波的波长是4m.
(2)波向左传播时传播波速为v=$\frac{x}{t}$=$\frac{4n+3}{0.2}$=(20n+15)m/s;向右传播时传播波速为 v=$\frac{x}{t}$=(20n+5)m/s,(n=0,1,2…).
(3)若波向左传播时波速为35m/s,55m/s;若波向右传播时波速为25m/s,45m/s.
点评 本题是知道两个时刻的波形研究波传播的距离、波速、周期的问题,关键是理解波的周期性,运用数学知识列出通项式.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
19.将弹簧的一端固定,从原长状态开始时弹簧的一端施加一个拉力,则弹簧伸长一段距离,在此过程中( )
| A. | 拉力对弹簧做正功,弹簧的弹性势能增大 | |
| B. | 拉力时弹簧做正功,弹簧的弹性势能减小 | |
| C. | 弹簧的弹力做正功,弹簧的弹性势能增大 | |
| D. | 弹簧的弹力做负功,弹簧的弹性势能减小 |
16.在静电场中,一个负电荷 受到非静电力作用由一条电场线上的A点移到B点,以下说法中正确的是( )
| A. | 非静电力和电场力对电荷做功之和等于电荷电势能增加量和动能增加量之和 | |
| B. | 非静电力做功等于电荷电势能和动能的增加量之和 | |
| C. | 电荷克服电场力做功等于电荷电势能的增加量 | |
| D. | 非静电力和电场力做功之和等于电荷动能增加量 |
13.下列说法中正确的是( )
| A. | 质点就是用一个点表示物体,没有质量 | |
| B. | 研究乒乓球在空中飞旋的轨迹可以把乒乓球看成质点 | |
| C. | 参考系必须选择静止不动的物体 | |
| D. | 作息时间表上的7:40表示的是时间 |
20.汽车从A点由静止开始沿直线ACB做匀变速直线运动,第4s末到达C点并关闭发动机匀减速前进,再经6s到达B点停止.已知AB长为30m,则下列说法正确的是( )
| A. | 通过C点时速度大小为6m/s | |
| B. | BC段位移为12m | |
| C. | 第5s末的速度大小为2m/s | |
| D. | 汽车在AC段平均速度大于CB段平均速度 |
17.竖直升空的火箭,其速度-时间图象如图所示,由图可知以下说法正确的是( )


| A. | 火箭在40s时速度方向发生变化 | B. | 火箭经过40s到达最高点 | ||
| C. | 火箭经过120s落回地面 | D. | 火箭上升的最大高度为48000m |
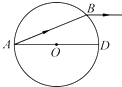 如图所示,一玻璃球体半径为R,0为球心,AD为水平直径.来自A点的彩色光从B点射出,射出光平行于AD.已知玻璃对此光的折射率为$\sqrt{3}$.若真空中光的传播速度为c,求此光从A到B的传播时间t.
如图所示,一玻璃球体半径为R,0为球心,AD为水平直径.来自A点的彩色光从B点射出,射出光平行于AD.已知玻璃对此光的折射率为$\sqrt{3}$.若真空中光的传播速度为c,求此光从A到B的传播时间t.