题目内容
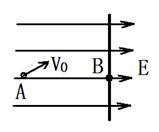
 在足够大的真空空间中,存在着水平向右的匀强电场,若用绝缘细线将质量为m的带正电的小球悬挂在电场中,静止时细线与竖直方向夹角θ=37°.现将该小球从电场的某点竖直向上抛出,抛出的初速度大小为υ0,如图所示.(sin37°=0.6,cos37°=0.8)求:
在足够大的真空空间中,存在着水平向右的匀强电场,若用绝缘细线将质量为m的带正电的小球悬挂在电场中,静止时细线与竖直方向夹角θ=37°.现将该小球从电场的某点竖直向上抛出,抛出的初速度大小为υ0,如图所示.(sin37°=0.6,cos37°=0.8)求:(1)小球受到的电场力的大小及方向
(2)小球从抛出点至最高点的电势能变化量
(3)小球在电场中运动过程中的最小速率.
分析:(1)静止时受重力,电场力,绳的拉力三力平衡,由数学关系可得电场力.
(2)小球从抛出点至最高点的过程中,由竖直方向的匀减速运动可得运动时间,在由水平方向做匀加速直线运动可得小球沿电场线方向的位移,进而可得电场力做的功,电场力做功电势能变化,可确定电势能变化量.
(3)撤去细线,现将该小球从电场中的A点竖直向上抛出,带电小球在水平方向的匀强电场中竖直向上抛出,小球在竖直方向受到重力,在水平方向受到电场力,从而做曲线运动,因此可将曲线分解成竖直方向与水平方向的两个运动.利用运动学公式可求出小球速率最小值;
(2)小球从抛出点至最高点的过程中,由竖直方向的匀减速运动可得运动时间,在由水平方向做匀加速直线运动可得小球沿电场线方向的位移,进而可得电场力做的功,电场力做功电势能变化,可确定电势能变化量.
(3)撤去细线,现将该小球从电场中的A点竖直向上抛出,带电小球在水平方向的匀强电场中竖直向上抛出,小球在竖直方向受到重力,在水平方向受到电场力,从而做曲线运动,因此可将曲线分解成竖直方向与水平方向的两个运动.利用运动学公式可求出小球速率最小值;
解答:解:
(1)静止时受重力,电场力,绳的拉力三力平衡,可得电场力等于:
F=mgtan37°=
mg
电场力的方向水平向右.
(2)小球沿竖直方向做匀减速运动,速度为vy,可得:
vy=v0-gt
解得小球上升到最高点的时间:
t=
沿水平方向做初速度为0的匀加速运动,加速度为ax,由牛顿第二定律得:
ax=
=
mg
此过程小球沿电场方向位移为:
sx=
axt2=
电场力做功:
W=Fsx=
mv02
电场力做正功电势能减少,故小球上升到最高点的过程中,电势能减少
mv02
(3)水平速度:
vx=axt
竖直速度:
vy=v0-gt
小球的速度:;
 v=
v=
由以上各式得出:
g2t2-2v0gt+(v02-v2)=0
解得当t=
时,v有最小值:
vmin=
v0
或者:
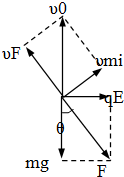
小球在电场中静止时有,重力与电场力的合力与细线的拉力是一对平衡力,力的合成如图所示.当小球以速度υ0竖直上抛时,将其速度分解到合力力的方向及与合外力垂直的方向,由图可知,当合外力使υF减速为零时,小球具有最小的速度为υmin=υ0sinθ=
v0.
答:
(1)小球受到的电场力的大小为
mg,方向水平向右.
(2)小球从抛出点至最高点的电势能减少
mv02.
(3)小球在电场中运动过程中的最小速率为
v0.
(1)静止时受重力,电场力,绳的拉力三力平衡,可得电场力等于:
F=mgtan37°=
| 3 |
| 4 |
电场力的方向水平向右.
(2)小球沿竖直方向做匀减速运动,速度为vy,可得:
vy=v0-gt
解得小球上升到最高点的时间:
t=
| v0 |
| g |
沿水平方向做初速度为0的匀加速运动,加速度为ax,由牛顿第二定律得:
ax=
| F |
| m |
| 3 |
| 4 |
此过程小球沿电场方向位移为:
sx=
| 1 |
| 2 |
| 3v0 |
| 8g |
电场力做功:
W=Fsx=
| 9 |
| 32 |
电场力做正功电势能减少,故小球上升到最高点的过程中,电势能减少
| 9 |
| 32 |
(3)水平速度:
vx=axt
竖直速度:
vy=v0-gt
小球的速度:;
 v=
v=| vx2+vy2 |
由以上各式得出:
| 25 |
| 16 |
解得当t=
| 16v0 |
| 25g |
vmin=
| 3 |
| 5 |
或者:
小球在电场中静止时有,重力与电场力的合力与细线的拉力是一对平衡力,力的合成如图所示.当小球以速度υ0竖直上抛时,将其速度分解到合力力的方向及与合外力垂直的方向,由图可知,当合外力使υF减速为零时,小球具有最小的速度为υmin=υ0sinθ=
| 3 |
| 5 |
答:
(1)小球受到的电场力的大小为
| 3 |
| 4 |
(2)小球从抛出点至最高点的电势能减少
| 9 |
| 32 |
(3)小球在电场中运动过程中的最小速率为
| 3 |
| 5 |
点评:考查了运动的合成与分解研究的方法,并让学生掌握运动学公式、牛顿第二定律、动能定理等规律.同时让学生形成如何处理曲线的方法.如果将速度按照合力方向和垂直合力方向分解,当沿合力方向的速度减为零时其速度达到最小值,也可以解出最小速度.运用速度矢量合成的三角形法则也可求解.

练习册系列答案
相关题目
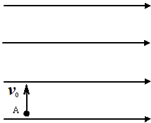 如图,在足够大的真空空间中,存在水平向右的匀强电场,若用绝缘细线将质量为m的带正电小球悬挂在电场中,静止时细线与竖直方向夹角θ=37°.撤去细线,现将该小球从电场中的A点竖直向上抛出,抛出的初速度大小为v0,已知sin37°=0.6,cos37°=0.8,求:
如图,在足够大的真空空间中,存在水平向右的匀强电场,若用绝缘细线将质量为m的带正电小球悬挂在电场中,静止时细线与竖直方向夹角θ=37°.撤去细线,现将该小球从电场中的A点竖直向上抛出,抛出的初速度大小为v0,已知sin37°=0.6,cos37°=0.8,求:
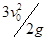 的B处放置,板上涂有特殊的物质,带电小球打到板上会使该物质持续发光。从第一个小球达到板上开始,板会缓慢向左平移直至A点,忽略电荷对电场的影响,小球可以看成质点,求板上的发光部分的长度?(
的B处放置,板上涂有特殊的物质,带电小球打到板上会使该物质持续发光。从第一个小球达到板上开始,板会缓慢向左平移直至A点,忽略电荷对电场的影响,小球可以看成质点,求板上的发光部分的长度?(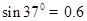 、
、 )
)