题目内容
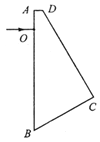
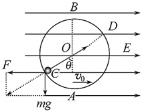
【题目】如图所示,在竖直平面内固定的圆形绝缘轨道的圆心在O点,半径为r,内壁光滑,A、B两点分别是圆弧的最低点和最高点。该区间存在方向水平向右的匀强电场,一质量为m、带负电的小球在轨道内侧做完整的圆周运动(电荷量不变),经C点时速度最大,O、C连线与竖直方向夹角θ=60°,重力加速度为g.

(1)求小球所受到的电场力大小;
(2)小球在A点速度多大时,小球经B点时对轨道的压力最小?
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)抓住带电小球运动至C点的速度最大这一突破口,根据竖直平面内圆周运动的最大速度出现在物理“最低点”,即合外力沿半径指向圆心,而电场力和重力的合力则背离圆心的方向。作出受力示意图,求解电场力的大小。(2)D点竖直平面内圆周运动的物理“最高点”,恰好能完整的做圆周运动,在“最高点”有最小速度,在“最高点”对轨道压力为0,由牛顿第二定律求解.
(1)已知带电小球在光滑的竖直圆轨道内做完整的圆周运动,经C点时速度最大,因此,C点是竖直平面内圆周运动的物理“最低点”,也就是小球在C点电场力和重力的合力则背离圆心的方向,如图:
则有![]()
因此电场力为:![]()
(2)D点竖直平面内圆周运动的物理“最高点”,恰好能完整的做圆周运动,在“最高点”有最小速度,即:![]()
解得:![]()
由A点运动到D点的过程,由动能定理:![]()
解得:![]()

练习册系列答案
相关题目