题目内容
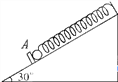
【题目】如图所示，一传送带与水平面的夹角为30°，以v0=2m/s的初速度按图示方向匀加速1s后再做匀速运动，加速时的加速度为1m/s2 ． 现将一质量为10kg的质点小工件轻放于传送带底端皮带，经一段时间后送到高2m的平台上，工件与传送带间的动摩擦因数为μ= 
，取g=10m/s2 ． 求：电动机由于传送工件多消耗的电能．
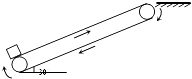
【答案】解：设工件向上运动的距离x时，速度达到传送带的速度v，由动能定理可知，此过程中有重力和摩擦力对工件做功： 
代入数据可解得：x= 
=1.8m
故工件未达到平台时，速度已达到v，
所以在此过程中，工件动能的增量为： 
=45J
势能的增加量为：△Ep=mgh=10×10×2J=200J
工件在加速运动过程中的工件的位移：x= = 
=1.8m
传送带的位移为：x′=vt
所以可知，x′=3.6m
所以在皮带上滑过程中由于滑动摩擦力做功而增加的内能：Q=μmgcosθ（x′﹣x）=135J
根据能量守恒定律知，电动机多消耗的电能为：E=△Ek+△Ep+Q=45J+200J+135J=380J
答：电动机由于传送工件多消耗的电能为380J
【解析】本题的关键是根据能量守恒定律，多消耗的电能应是煤块增加的机械能与系统产生的热量之和．关键是物体由底端运送到平台上需要经过匀加速和匀速两个过程需要分过程分析．
【考点精析】通过灵活运用功能关系和能量守恒定律，掌握当只有重力（或弹簧弹力）做功时，物体的机械能守恒；重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2；合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 （动能定理）；除了重力（或弹簧弹力）之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1；能量守恒定律：能量既不会消灭，也不会创生，它只会从一种形式转化为其他形式，或者从一个物体转移到另一个物体，而在转化和转移过程中，能量的总量保持不变即可以解答此题．
