题目内容
一矿井深为125m，在井口每隔一定时间自由下落一个小球，当第11个小球刚从井口下落时，第1个小球恰好到井底．则相邻两个小球开始下落的时间间隔为 s，这时第10个小球和第8个小球相隔 m．（g=10m/s2）
【答案】分析：由自由落体的位移公式由h=
gt2可求得位移为125m所用的总时间，11个小球共10个间隔△t=
；
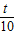第10个小球的位移与第8个小球位移之差△H=H10-H8=
g（t12-t22）即可求解．
解答：解：（1）设小球自由下落到达井底经历时间为t，则
由 H=
gt2
得 t=5s
所以相邻两个小球见的时间间隔为
△t=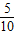
=0.5s
（2）由以上计算可知，当第一个小球到达井底时第三个小球刚好下落t1=4s，第五个小球刚好下落t2=3s故△H=H10-H8=
g（t12-t22）=10m
△H=10m
答：（1）相邻两个小球开始下落的时间间隔为0.5s
（2）这时第3个小球和第5个小球相隔的距离为10m
故答案为：0.5；10．
点评：解决自由落体运动的题目关键在于明确自由落体中的公式应用，一般情况下，研究由落点开始的运动列出的表达式最为简单．
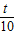gt2可求得位移为125m所用的总时间，11个小球共10个间隔△t=；第10个小球的位移与第8个小球位移之差△H=H10-H8=
g（t12-t22）即可求解．解答：解：（1）设小球自由下落到达井底经历时间为t，则
由 H=
gt2 得 t=5s
所以相邻两个小球见的时间间隔为
△t=
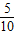=0.5s （2）由以上计算可知，当第一个小球到达井底时第三个小球刚好下落t1=4s，第五个小球刚好下落t2=3s故△H=H10-H8=
g（t12-t22）=10m△H=10m
答：（1）相邻两个小球开始下落的时间间隔为0.5s
（2）这时第3个小球和第5个小球相隔的距离为10m
故答案为：0.5；10．
点评：解决自由落体运动的题目关键在于明确自由落体中的公式应用，一般情况下，研究由落点开始的运动列出的表达式最为简单．
练习册系列答案
阅读快车系列答案
相关题目