Question

【题目】如图，在地面上方某处足够大的真空室里存在着水平向右的匀强电场，分别以水平向右、竖直向下和水平向里建立坐标系Oxyz（z轴未画出）。一质量为m、带电量为-q的微粒从点P（l，0，0）处静止释放后沿直线PQ运动，经过时间t时，微粒运动到点。

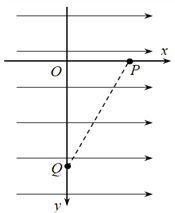
(1)求匀强电场的场强E和重力加速度g的大小；

(2)若把该微粒从P点以某一速度抛出，经过时间时，微粒恰好经过O点，求微粒经过O点时的动能Ek ；

(3)若撤去电场，在整个空间加上沿y轴正方向、磁感强度大小为B的匀强磁场，且该微粒从O点沿x轴正方向以一定速度抛出，求微粒经过y轴时离O点距离的可能值。

Answer 1

【答案】(1), (2) (3) (n=1,2,3,…)

【解析】（1）设微粒从P到Q的位移为S，∠OPQ为θ，由几何关系得

①

tanθ= θ=60° ②

由位移公式得S=at2 ③

由匀加速度直线运动条件可得 ④

由①②③④式得 ⑤

根据匀加速度直线运动条件可得mg=masinθ ⑥

由①②③⑥式得 ⑦

（2）设沿PQ方向运动的速度为v1，由位移公式得

⑧

由③⑧式得 v1=0 ⑨

可知微粒沿垂直PQ向上抛出，微粒做类平抛运动，如图，

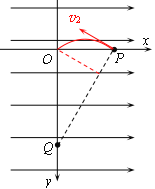
设抛出速度为v2，在抛出方向上微粒做匀速直线运动有 ⑩

从P至O过程，由动能定理得

由②⑤⑧⑨式得

（3）设抛出的速度为v3，水平方向合力是洛伦兹力，竖直方向合力是重力，可知微粒在水平方向做匀速圆周运动，在竖直方向做自由落体运动

水平面内，由牛顿第二定律得

匀速圆周运动周期

竖直方向，与y轴交点与O的距离为y，则 (n=1，2，3，…)

由⑦⑩式得 (n=1，2，3，…)