题目内容
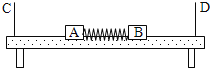
【题目】光滑水平面上有一质量为M滑块，滑块的左侧是一光滑的圆弧，圆弧半径为R＝1m。一质量为m的小球以速度v0向右运动冲上滑块。已知M＝4m，g取10m／s2若小球刚好没跃出
圆弧的上端，求：
（1）小球的初速度v0是多少?
（2）滑块获得的最大速度是多少?
【答案】（1）5m/s（2）2m/s
【解析】试题分析：（1）当小球上升到滑块上端时，小球与滑块水平方向速度相同，设为v1，以小球的初速度方向为正方向，在水平方向上，由动量守恒定律得：mv0=（m+M）v1…①
由机械能守恒定律得： 
mv02=
（m+M）v12+mgR …②，
代入数据解得：v0=5m/s …③；
（2）小球到达最高点以后又滑回，滑块又做加速运动，当小球离开滑块后滑块速度最大．研究小球开始冲上滑块一直到离开滑块的过程，以小球的初速度方向为正方向，由动量守恒定律得：
mv0=mv2+Mv3…④
由机械能守恒定律得： 
mv02=
mv22+
Mv32…⑤
解得： 
…⑥
练习册系列答案
相关题目
