题目内容
【题目】长为L=2m的细线,拴一质量为m=0.2kg的小球,一端固定于O点.让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图所示.当摆线与竖直方向的夹角为α=37°时,不计空气阻力.(取 sin 37°=0.60,cos 37°=0.80;g取 10 m/s2)求:
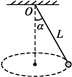
(1)细线的拉力F的大小.
(2)小球运动的线速度大小.
(3)小球运动的角速度及周期.
【答案】(1)2.5N(2)3m/s(3)0.8s
【解析】(1)对小球受力分析如图所示,小球受重力mg和绳子的拉力F.因为小球在水平面内做匀速圆周运动,所以小球受到的合力指向圆心O',且沿水平方向.由平行四边形定则得小球受到的合力大小为mgtan α

细线对小球的拉力大小为 ![]()
(2)由牛顿第二定律得![]()
由几何关系得r=Lsinα=1.2m
所以小球做匀速圆周运动的线速度的大小为v=3m/s
(3)v=ωr
ω=2.5rad/s
小球运动的周期![]()

练习册系列答案
相关题目