题目内容
(10分)如图所示,AB是一段位于竖直平面内的弧形轨道,高度为h,末端B处的切线沿水平方向。一个质量为m的小物体P(可视为质点)从轨道顶端处A点由静止释放,滑到B点时以水平速度v飞出,落在水平地面的C点,其轨迹如图中虚线BC所示。已知P落地时相对于B点的水平位移OC=l,重力加速度为g,不计空气阻力的作用。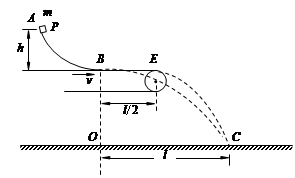
(1)请计算P在弧形轨道上滑行的过程中克服摩擦力所做的功;
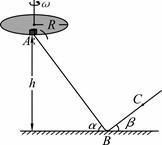
(2)现于轨道下方紧贴B点安装一水平传送带,传送带右端E轮正上方与B点相距。先将驱动轮锁定,传送带处于静止状态。使P仍从A点处由静止释放,它离开B点后先在传送带上滑行,然后从传送带右端水平飞出,恰好仍落在地面上C点,其轨迹如图中虚线EC所示。若将驱动轮的锁定解除,并使驱动轮以角速度ω顺时针匀速转动,再使P仍从A点处由静止释放,最后P的落地点是D点(图中未画出)。已知驱动轮的半径为r,传送带与驱动轮之间不打滑,且传送带的厚度忽略不计。求:
①小物块P与传送带之间的动摩擦因数;
②若驱动轮以不同的角速度匀速转动,可得到与角速度ω对应的OD值,讨论OD的可能值与ω的对应关系。
(1)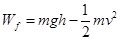 ;
;
(2)①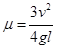 ;
;
②当0﹤ω﹤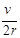 时,OD=l;当ω﹥
时,OD=l;当ω﹥ 时,OD=(
时,OD=(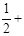
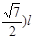 ;当
;当 ﹤ω﹤
﹤ω﹤ 时,OD=
时,OD= 。
。
解析试题分析:(1)小物块从A到B的过程中有重力和摩擦力对其做功,
故根据动能定理有: (2分)
(2分)
解得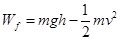 (1分)
(1分)
(2)① 需要先求出物块在E点的速度;
没有安装传送带时,小物块从B到C的过程,做平抛运动,水平方向有l=vt;
安装传送带后,小物块从E到C的过程沿水平方向有l/2=vEt,二者的竖直高度相等,落下时所用的时间相等,故联立以上两个方程,解得vE=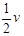 (1分)
(1分)
设小物块与传送带之间的动摩擦因数为μ,小物块从B到E的过程,根据动能定理有
-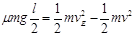 (2分)
(2分)
解得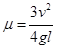 (1分)
(1分)
②(a)当传送带的速度0﹤v带=ωr﹤vE,
即0﹤ω﹤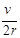 时,物体在传送带上一直做匀减速运动,物体离开传送带时的速度为vE,则OD=l…(1分)
时,物体在传送带上一直做匀减速运动,物体离开传送带时的速度为vE,则OD=l…(1分)
(b)如果传送带的速度较快,物体在传送带上一直加速而未与传送带共速,则物体的加速度始终为a=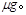 设物体离开传送带时的速度为vmax,
设物体离开传送带时的速度为vmax,
根据运动学公式有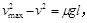 解得vmax=
解得vmax=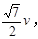
当传送带的速度v带=ωr﹥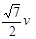 ,
,
即ω﹥ 时,物体离开传送带点时的速度为vmax,
时,物体离开传送带点时的速度为vmax,
则OD=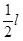 +
+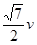 t=(
t=(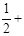
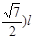 …(1分)
…(1分)
(c)当传送带的速度vE﹤v带=ωr﹤vmax,
即 ﹤ω﹤
﹤ω﹤ 时,物体离开传送带点时的速度为v带=ωr,则OD=
时,物体离开传送带点时的速度为v带=ωr,则OD=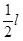 +ωrt=
+ωrt= …(1分)
…(1分)
考点:动能定理,牛顿第二定律,运动学公式在传送带问题上的综合应用。

一物体受绳的拉力作用由静止开始前进,先做加速运动,然后改做匀速运动,再改做减速运动,则下列说法中正确的是( )
| A.加速前进时,绳拉物体的力大于物体拉绳的力 |
| B.减速前进时,绳拉物体的力大于物体拉绳的力 |
| C.只有匀速前进时,绳拉物体的力与物体拉绳的力大小才相等 |
| D.不管物体如何前进,绳拉物体的力与物体拉绳的力大小总相等 |
2013年12月2日1时30分,搭载月球车和着陆器的嫦娥三号月球探测器从西昌卫星发射中心升空,飞行约18min后,嫦娥三号进入如图所示的地月转移轨道AB,A为入口点,B为出口点,嫦娥三号在B点经过近月制动,进入距离月面h=100公里的环月圆轨道,其运行的周期为T,然后择机在月球虹湾地区实行软着陆,展开月面巡视勘察。若以R表示月球半径,忽略月球自转及地球对它的影响。下列说法正确的是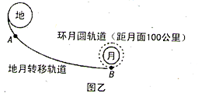
| A.携带月球车的着陆器在月球上着陆过程中一直处于失重状态 |
B.物体在月球表面自由下落的加速度大小为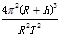 |
C.月球的第一宇宙速度为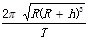 |
| D.由于月球表面重力加速度较小,故月球车在月球上执行巡视探测任务时处于失重状态 |
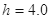 m。一架质量为
m。一架质量为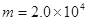 kg的飞机,其喷气发动机的推力大小恒为
kg的飞机,其喷气发动机的推力大小恒为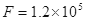 N,方向与速度方向相同,在运动过程中飞机受到的平均阻力大小为飞机重力的0.1倍,假设航母处于静止状态,飞机质量视为不变并可看成质点,倾斜跑道看作斜面,不计拐角处的影响。取
N,方向与速度方向相同,在运动过程中飞机受到的平均阻力大小为飞机重力的0.1倍,假设航母处于静止状态,飞机质量视为不变并可看成质点,倾斜跑道看作斜面,不计拐角处的影响。取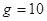 m/s2。
m/s2。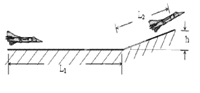
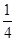 圆弧轨道固定在水平地面上,O为该圆弧的圆心,轨道上方的A处有一个可视为质点的质量m=1 kg的小物块,小物块由静止开始下落后恰好沿切线进入
圆弧轨道固定在水平地面上,O为该圆弧的圆心,轨道上方的A处有一个可视为质点的质量m=1 kg的小物块,小物块由静止开始下落后恰好沿切线进入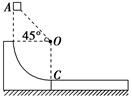
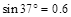 ,
,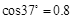 。求:
。求: